Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

thay x,y vô hệ đã cho rồi giải hệ với nghiệm a,b là ra ak bạn
8-a=b
2+b=a
(a;b)=(5;3)

Lời giải:
a) Phương trình hoành độ giao điểm:
\(-x+2=x^2\\\Rightarrow x^2=-x+2\\ \Rightarrow x^2+x-2=0\\ \Rightarrow x^2+2x-x-2=0\\ \Rightarrow x\left(x+2\right)-\left(x+2\right)=0\\ \Rightarrow\left(x+2\right)\left(x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x+2=0\\x-1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)
Thay \(x=-2\) vào \(y=x^2\), ta được: \(y=\left(-2\right)^2=4\)
Thay \(x=1\) vào \(y=x^2\), ta được: \(y=1^2=1\)
Vậy \(\left\{{}\begin{matrix}A\left(-2;4\right)\\B\left(1;1\right)\end{matrix}\right.\)
b) Theo đề bài ta có hệ phương trình: \(\left\{{}\begin{matrix}4.2+a.\left(-1\right)=b\\2-b.\left(-1\right)=a\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}8-a=b\\2+b=a\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}-a-b=-8\\-a+b=-2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-2b=-6\\-a+b=-2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=3\\-a+3=-2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=3\\a=5\end{matrix}\right.\)
Vậy a = 5, b = 3 thì hệ phương trình có nghiệm duy nhất \(\left(x;y\right)=\left(2;-1\right)\)

1:
a)\(\hept{\begin{cases}nx+x=5
\\x+y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x.\left(n+1\right)=5\left(1\right)\\x+y=1\end{cases}}\)

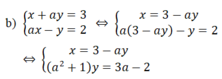
Do a 2 + 1 ≠ 0 ∀ x nên hệ phương trình trở thành:
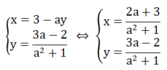
Khi đó:
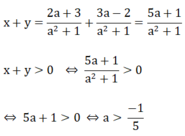
Vậy với a > (-1)/5 thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x+y >0