Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Để hệ phương trình có nghiệm duy nhất
\(\Leftrightarrow\dfrac{a}{1}\ne-\dfrac{1}{a}\)
\(\Leftrightarrow a^2\ne-1\) ( Luôn đúng )
Vậy mọi a thuộc R hệ phương trình luôn có 1 nghiệm duy nhất .
- Ta có : \(\left\{{}\begin{matrix}y=ax-2\\x+a\left(ax-2\right)=3\end{matrix}\right.\)
- Từ PT ( II ) => \(x+xa^2-2a=3\)
\(\Rightarrow x=\dfrac{2a+3}{a^2+1}\)
- Thay lại x vào PT ( I ) ta được : \(y=\dfrac{a\left(2a+3\right)}{a^2+1}-2\)
\(=\dfrac{2a^2+3a-2a^2-2}{a^2+1}=\dfrac{3a-2}{a^2+1}\)
Vậy ...

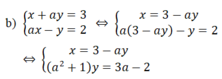
Do a 2 + 1 ≠ 0 ∀ x nên hệ phương trình trở thành:
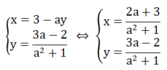
Khi đó:
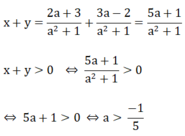
Vậy với a > (-1)/5 thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x+y >0

Lời giải:
a) $x+ay=1\Rightarrow x=1-ay$. Thay vào PT $(2)$ có:
$-a(1-ay)+y=a$
$\Leftrightarrow y(1+a^2)=2a(*)$
Vì $1+a^2\neq 0$ với mọi $a\in\mathbb{R}$ nên PT $(*)$ có nghiệm $y=\frac{2a}{a^2+1}$ duy nhất.
Kéo theo HPT ban đầu có nghiệm $(x,y)$ duy nhất với mọi $a$
b) $y=\frac{2a}{a^2+1}$ nên $x=1-ay=1-\frac{2a^2}{a^2+1}=\frac{1-a^2}{a^2+1}$
Để \(x< 1; y< 1\Leftrightarrow \left\{\begin{matrix} \frac{2a}{a^2+1}< 1\\ \frac{1-a^2}{a^2+1}< 1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2a< a^2+1\\ 1-a^2< a^2+1\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} a^2+1-2a>0\\ 2a^2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (a-1)^2>0\\ a^2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a\neq 1\\ a\neq 0\end{matrix}\right.\)
cho hệ phương trình{6x+ay=6 và 2ax+by=3
- giải hệ phương trình khi a=b=1
- tìm a,b để hệ có nghiệm x=1,y=5

6x+ay=6, 2ax+by=3
Thay a=b=1 vào hệ phương trình ta có 6x+y=6, 2x+y=3
6x+y-(2x+y)=6-3
4x=3
x=3/4
y=6-6.3/4=3/2
Vì hệ có nghiệm x=1,y=5 nên ta có 6.1+a.5=6 và 2a+5b=3
a.5=0
a=0
Thay a=0 vào 2a+5b=3 ta có 0+5b=3 =>b=3/5
thay x,y vô hệ đã cho rồi giải hệ với nghiệm a,b là ra ak bạn
8-a=b
2+b=a
(a;b)=(5;3)