Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b:ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của MN

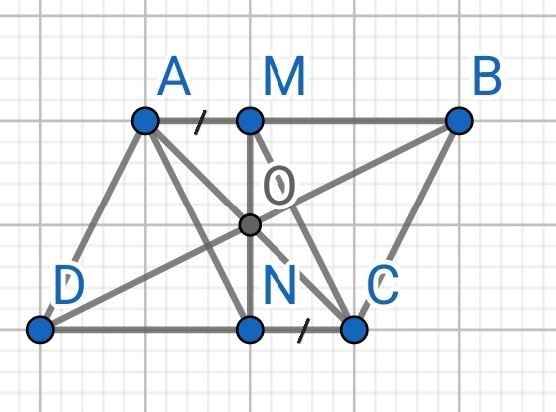 a) Do ABCD là hình bình hành
a) Do ABCD là hình bình hành
AB // CD
⇒ AM // CN
Tứ giác AMCN có:
AM // CN (cmt)
AM = CN (gt)
⇒ AMCN là hình bình hành
⇒ AN // CM
b) Do ABCD là hình bình hành
O là giao điểm của AC và BD
⇒ O là trung điểm của AC
Lại có AMCN là hình bình hành
O là trung điểm của AC (cmt)
⇒ O là trung điểm của MN

A B C D E N F M I
a) - Xét \(\Delta AME\) và \(\Delta CNF\) có :
+ AM = CN (GT)
+ \(\widehat{MAE}=\widehat{NCF}\)(GT)
+ AE = CF ( GT )
=> \(\Delta AME=\Delta CNF\left(c.g.c\right)\) => ME = NF ( 2 cạnh tương ứng bằng nhau )
- Tương tự , \(\Delta DMF=\Delta BNE\left(c.g.c\right)\) => MF = NE ( 2 cạnh tương ứng bằng nhau )
- Xét tứ giác EMFN có :
+ ME = NF
+ MF = NE
=> EMFN là hình bình hành ( 2 cặp cạnh đối bằng nhau )
b) Vì ABCD là Hình bình hành => AC cắt BD tại I => I là trung điểm của AC , BD (1)
Tương tự AC cắt EF và MN tại trung điểm I của AC (2)
Từ 1 và 2 => EF và MN đều đi qua I


a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b:ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của MN