Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b:ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của MN

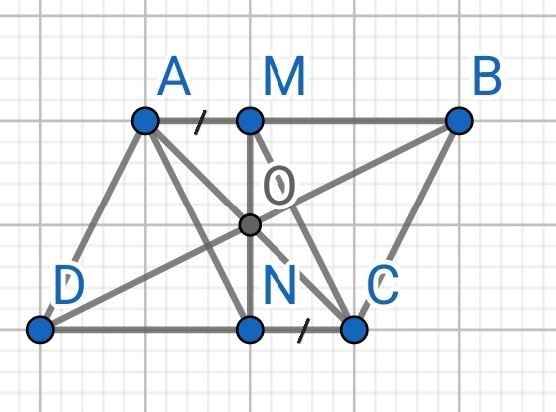 a) Do ABCD là hình bình hành
a) Do ABCD là hình bình hành
AB // CD
⇒ AM // CN
Tứ giác AMCN có:
AM // CN (cmt)
AM = CN (gt)
⇒ AMCN là hình bình hành
⇒ AN // CM
b) Do ABCD là hình bình hành
O là giao điểm của AC và BD
⇒ O là trung điểm của AC
Lại có AMCN là hình bình hành
O là trung điểm của AC (cmt)
⇒ O là trung điểm của MN

a)Ta có O giao điểm AC và BD trong hình bình hành ABCD (gt)
=> O là trung điểm AC và BD.
=> OD=OB
Mà OM=MD=\(\frac{1}{2}\)OD; ON=BN=\(\frac{1}{2}\)OB => OM=ON=OD=OB.
Xét hình bình hành ABCD có O trung điểm AC (hbh ABCD) và O trung điểm MN (OM=ON)
=> đpcm (điều phải chứng minh)
b) C/m tam giác ACE=ACF (cgc)(AC chung; \(\angle EAC=\angle FCA\) do song song; và cũng như vây với \(\angle ECA=\angle CAF\))
=>AE=FC mà \(AE \parallel FC\) do ăn theo hbh AMCN => đpcm

( bạn tự vẽ hình nha )
a, Vì M nằm tren cạnh AB, N nằm trêm cạnh CD => AM \(//\) CN
Mà AM=CN ( Theo gt) . Do đó tứ giác AMCN là hình bình hành ( Theo đk 3)
b, Vì ABCD là hình bình hành => Góc A= Góc C
Xét 2 tam giác AMP và tam giác CNQ bằng nhau theo TH c-g-c ( Tự CM )
=> MP=NC( 2 cạnh tương ứng )(1)
CMTT 2 tam giác MBQ và NDP ta được MQ=PN (2)
Từ (1) và (2) ta có MPNQ là hình bình hành (đpcm)
a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành