Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ DI,DJ lần lượt vuông góc với AK,CK
\(a,S_{AND}=\dfrac{1}{2}AN\cdot DI=\dfrac{1}{2}S_{ABCD}\) (chung đáy AD, cùng chiều cao hạ từ N)
\(b,S_{CDM}=\dfrac{1}{2}CM\cdot DJ=\dfrac{1}{2}S_{ABCD}\) (chung đáy CD, cùng chiều cao hạ từ M)
\(\Rightarrow\dfrac{1}{2}AN\cdot DI=\dfrac{1}{2}CM\cdot DJ\Rightarrow DI=DJ\left(AN=CM\right)\\ \Rightarrow\Delta DIK=\Delta DJG\left(ch-cgv\right)\\ \Rightarrow\widehat{IKD}=\widehat{JKD}\)
Vậy KD là phân giác \(\widehat{AKC}\)

Cảm ơn bạn vì đã có ý giúp nhưng mình tìm được câu tương tự rồi. Cảm ơn bạn nhiều

Trước hết ta chứng minh bổ đề sau (nếu em chưa học)
Cho 4 điểm A; B; C; D phân biệt sao cho \(AB||CD\), khi đó ta luôn có: \(S_{\Delta ACD}=S_{\Delta BCD}\)
C/m: từ A và B lần lượt kẻ \(AH\) và \(BK\) vuông góc CD \(\Rightarrow AH||BK\Rightarrow\) tứ giác AHKB là hình chữ nhật
\(\Rightarrow AH=BK\)
Do \(\left\{{}\begin{matrix}S_{\Delta ACD}=\dfrac{1}{2}AH.CD\\S_{\Delta BCD}=\dfrac{1}{2}BK.CD\end{matrix}\right.\) mà \(AH=BK\Rightarrow S_{\Delta ACD}=S_{\Delta BCD}\) (đpcm)
Quay lại bài toán, áp dụng bổ đề trên ta có: do N thuộc BC nên \(NC||AD\Rightarrow S_{\Delta NAD}=S_{\Delta CAD}\) (1)
Tương tự, \(AM||CD\Rightarrow S_{\Delta ACD}=S_{\Delta MCD}\) (2)
(1);(2) \(\Rightarrow S_{\Delta NAD}=S_{\Delta MCD}\)
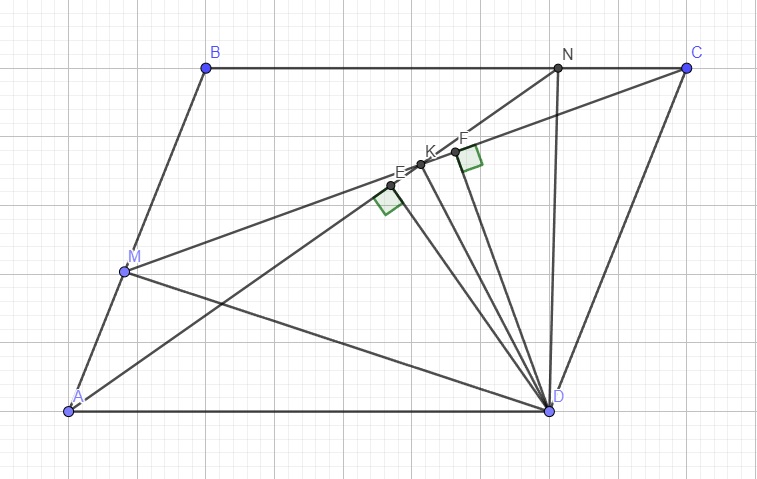
Từ D lần lượt kẻ \(DE\perp AN\) và \(DF\perp CM\)
\(\Rightarrow\left\{{}\begin{matrix}S_{\Delta NAD}=\dfrac{1}{2}DE.AN\\S_{\Delta MCD}=\dfrac{1}{2}DF.CM\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}S_{\Delta NAD}=S_{\Delta MCD}\\AN=CM\end{matrix}\right.\) \(\Rightarrow DE=DF\)
\(\Rightarrow\Delta_VDEK=\Delta_VDFK\left(ch-cgv\right)\)
\(\Rightarrow\widehat{EKD}=\widehat{FKD}\) hay KD là phân giác

Ta có: AM=MB=AB/2 ( M là trung điểm AB)
DN=NC=DC/2 (N là trung điểm DC)
Mà: AB=AC (ABCD LÀ HBH)
=> AM=MB=DN=NC
Xét tứ giác AMCN:
AM=NC (cmt)
AM//NC (AB//CD)
Vậy AMCN là hình bình hành
b.
Xét tứ giác AMND:
AM=ND (cmt)
AM//ND (AB//CD)
Vậy AMDN là hình bình hành
C. hình như bạn chép sai đề rồi: TK??

A B C D N M P Q
a) Ta có : \(\frac{S_{APQ}}{S_{AMN}}=\frac{S_{APQ}}{S_{APN}}.\frac{S_{APN}}{S_{AMN}}=\frac{AQ}{AN}.\frac{AP}{AM}\)
Ta cần tính tỉ số \(\frac{AQ}{AN},\frac{AP}{AM}\)
Thật vậy, ta có : \(\frac{AQ}{QN}=\frac{AB}{DN}=3\Rightarrow\frac{AQ}{AQ+QN}=\frac{3}{4}\Rightarrow\frac{AQ}{AN}=\frac{3}{4}\)
\(\frac{AP}{PM}=\frac{AD}{BM}=2\Rightarrow\frac{AP}{AP+PM}=\frac{2}{3}\Rightarrow\frac{AP}{AM}=\frac{2}{3}\)
Do đó : \(\frac{AQ}{AN}.\frac{AP}{AM}=\frac{3}{4}.\frac{2}{3}=\frac{1}{2}\)
Vậy \(S_{APQ}=\frac{1}{2}.S_{AMN}\)
b) Ta có : \(\frac{CN}{ND}=2.\frac{BM}{MC}\)
đặt \(\frac{BM}{MC}=k\)thì \(\frac{CN}{ND}=2k\)
Đặt MC = x thì BM = kx . đặt ND = y thì CN = 2ky
ta có : \(\frac{AP}{PM}=\frac{AD}{BM}=\frac{x+kx}{kx}=\frac{k+1}{k}\Rightarrow\frac{AP}{AP+PM}=\frac{k+1}{2k+1}\)
\(\Rightarrow\frac{AP}{AM}=\frac{k+1}{2k+1}\) ( 1 )
Mặt khác, \(\frac{AQ}{QN}=\frac{AB}{DN}=\frac{2k+1}{1}\Rightarrow\frac{AQ}{AQ+QN}=\frac{2k+1}{2k+2}\Rightarrow\frac{AQ}{AN}=\frac{2k+1}{2k+2}\) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra \(\frac{AP}{AM}.\frac{AQ}{AN}=\frac{k+1}{2k+1}.\frac{2k+1}{2k+2}=\frac{1}{2}\)
Vậy \(S_{APQ}=\frac{1}{2}.S_{AMN}\)