Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a. Ta có : \(y'=3x^2-6x+2\)
\(x_0=1\Leftrightarrow y_0=-6\) và \(y'\left(x_0\right)=y'\left(-1\right)=11\)
Suy ra phương trình tiếp tuyến là \(y=y'\left(-1\right)\left(x+1\right)-6=11x+5\)
b. Gọi \(M\left(x_0;6\right)\) là tiếp điểm, ta có :
\(x_0^3-3x_0^2+2x_0=6\Leftrightarrow\left(x_0-3\right)\left(x_0^2+2\right)=0\Leftrightarrow x_0=3\)
Vậy phương trình tiếp tuyến là :
\(y=y'\left(3\right)\left(x-3\right)+6=11x-27\)
c. PTHD giao điểm của (C) với Ox :
\(x^3-3x^2+2x=0\Leftrightarrow x=0;x=1;x=2\)
* \(x=0\) ta có tiếp tuyến : \(y=y'\left(0\right)\left(x-0\right)+0=2x\)
* \(x=1\) ta có tiếp tuyến : \(y=y'\left(1\right)\left(x-1\right)+0=-x+1\)
* \(x=2\) ta có tiếp tuyến : \(y=y'\left(2\right)\left(x-2\right)+0=2x-4\)
Với m = 1, ta có \(\left(C_1\right):y=\frac{x+1}{x-1}\)
a. Gọi d là đường thẳng đi qua P, có hệ số góc k => \(d:y=k\left(x-3\right)+1\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}\frac{x+1}{x-1}=k\left(x-3\right)+1\\\frac{-2}{\left(x-1\right)^2}=k\end{cases}\) có nghiệm
Thế k vào phương trình thứ nhất, ta được :
\(\frac{x+1}{x-1}=\frac{-2}{\left(x-1\right)^2}\left(x-3\right)+1\Leftrightarrow x=2\)
\(\Rightarrow k=-2\Rightarrow\) phương trình tiếp tuyến : \(y=-2x+7\)
b. Gọi d là đường thẳng đi qua A, có hệ số góc k : \(d:y=k\left(x-2\right)-1\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}\frac{x+1}{x-1}=k\left(x-2\right)-1\\\frac{-2}{\left(x-1\right)^2}=k\end{cases}\) có nghiệm
Thế k vào phương trình thứ nhất, ta được :
\(\frac{x+1}{x-1}=\frac{-2}{\left(x-1\right)^2}\left(x-2\right)-1\Leftrightarrow x=\pm\sqrt{2}\)
* \(x=\sqrt{2}\Rightarrow k=-2\left(3+2\sqrt{2}\right)\Rightarrow\) phương trình tiếp tuyến : \(y=-2\left(3+2\sqrt{2}\right)x+11+8\sqrt{2}\)
* \(x=-\sqrt{2}\Rightarrow k=-2\left(3-2\sqrt{2}\right)\Rightarrow\) phương trình tiếp tuyến : \(y=-2\left(3-2\sqrt{2}\right)x+11-8\sqrt{2}\)
c. Ta có : \(y'=\frac{m^2-2m-1}{\left(x+m-2\right)^2}\)Tiếp tuyến tại điểm có hoành độ x = 1 vuông góc với đường thẳng\(y=x+1\Leftrightarrow y'\left(1\right)=-1\Leftrightarrow\frac{m^2-2m-1}{\left(m-1\right)^2}=-1\)\(\Leftrightarrow m=0;m=2\)
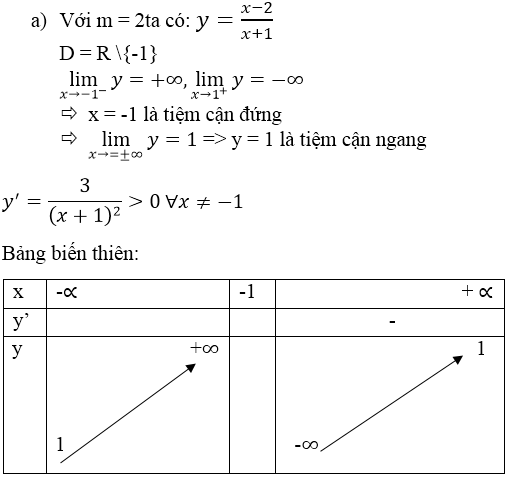
Gọi \(x_0\) là hoành độ tiếp điểm \(\left(x_0\ne-1\right)\), phương trình tiếp tuyến là :
\(y=\frac{1}{\left(x_0+1\right)^2}\left(x-x_0\right)+\frac{2x_0+1}{x_0+1}\)
Vì tiếp tuyến cách đều A và b nên tiếp tuyến đi qua trung điểm I của AB hoặc song song AB.
- Nếu tiếp tuyến đi qua trung điểm I(-1;1) của AB ta có \(x_0=1\), vậy phương trình là \(y=\frac{1}{4}x+\frac{5}{4}\)
- Nếu tiếp tuyến song song với đường thẳng AB : \(y=x+2\), ta có :
\(\frac{1}{\left(x_0+1\right)^2}=1;\frac{2x_0+1}{x_0+1}\ne2\Rightarrow x_0=0;x_0=-2\)
Với \(x_0=0\) ta có : \(y=x+1\)
Với \(x_0=-2\) ta có : \(y=x+5\)
\(y'=\dfrac{3}{\left(x+1\right)^2}\)
Gọi \(M\left(m;\dfrac{2m-1}{m+1}\right)\) là tiếp điểm
Phương trình tiếp tuyến tại M:
\(y=\dfrac{3}{\left(m+1\right)^2}\left(x-m\right)+\dfrac{2m-1}{m+1}\)
\(\Leftrightarrow3x-\left(m+1\right)^2y+2m^2-2m-1=0\)
Áp dụng công thức khoảng cách:
\(\dfrac{\left|-\left(m+1\right)^2+2m^2-2m-1\right|}{\sqrt{9+\left(m+1\right)^4}}=1\)
Bạn tự giải ra m nhé
.
.
.
.
Gọi 
là giao điểm của đồ thị hàm số (C) với trục Oy.
Khi đó ta có:
Ta có: 
Vậy phương trình tiếp tuyến của đồ thị hàm số (C) tại điểm 
là:
Chọn C
\(y'=-3x^2+3=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
\(x=-1\) là điểm cực tiểu
\(x=1\) là điểm cực đại
Hàm đồng biến trên \(\left(-1;1\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
BBT:
b. \(y'\left(2\right)=-9\)
Phương trình tiếp tuyến:
\(y=-9\left(x-2\right)+0\Rightarrow y=-9x+18\)
Phương trình hoành độ giao điểm của hai đường cong :
Phương trình (*) tương đương : 2 = 2x2 + 2 – x3 – x
⇔ x3 – 2x2 + x = 0 
( đều thỏa mãn khác 2).
Vậy tọa độ giao điểm của hai đường cong là A(0 ; 1) và B(1 ; 2)
+ Phương trình tiếp tuyến tại A là
+ Phương trình tiếp tuyến tại điểm B(1 ; 2) là :
y = y’(1). (x – 1) + 2 = 2(x – 1)+ 2
Hay y = 2x
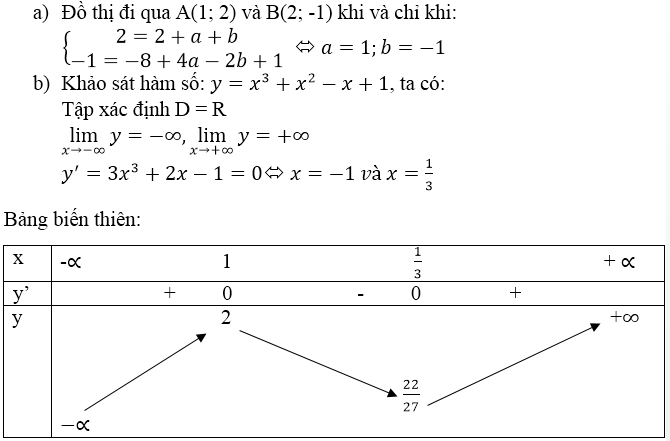
Ta có \(y=x^4-4x^3+4x^2\Rightarrow4x^3-12x^2+8x\)
a. PTHD giao điểm của (C) và Parabol \(y=x^2\) :
\(x^4-4x^3+4x^2=x^2\Leftrightarrow x^2\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow x=0;x=1;x=3\)
* \(x=0\) ta có phương trình tiếp tuyến là \(y=0\)
* \(x=2\) ta có phương trình tiếp tuyến là \(y=1\)
* \(x=3\) ta có phương trình tiếp tuyến là \(y=24x-63\)
b. Gọi d là đường thẳng đi qua A, có hệ số góc k \(\Rightarrow d:y=k\left(x-2\right)\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}\left(2-x\right)^2x^2-k\left(x-2\right)\\4x\left(x-2\right)\left(x-1\right)=k\end{cases}\) có nghiệm
Thay k vào phương trình thứ nhất ta có :
\(x^4-4x^3+4x^2=\left(x-2\right)\left(4x^3-12x^2+8x\right)\)
\(\Leftrightarrow x\left(3x-4\right)\left(x-2\right)^2=0\)
\(\Leftrightarrow x=0;x=2;x=\frac{4}{3}\)
* \(x=0\Rightarrow k=0\Rightarrow\) Phương trình tiếp tuyến \(y=0\)
* \(x=2\Rightarrow k=0\Rightarrow\) Phương trình tiếp tuyến \(y=0\)
* \(x=\frac{4}{3}\Rightarrow k=-\frac{32}{27}\Rightarrow\) Phương trình tiếp tuyến \(y=-\frac{32}{27}x+\frac{64}{27}\)