Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D.
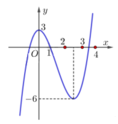
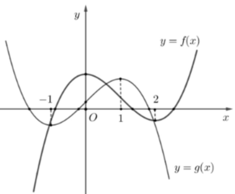
Kí hiệu trên đồ thị như hình bên.
Đặt u = f x . Ta có g x = f f x = f u .
g
'
x
=
u
'
.
f
'
u
=
f
'
x
.
f
'
u
g
'
x
=
0
⇔
f
'
x
=
0
f
'
u
=
0
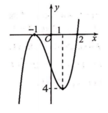
f ' x = 0 ⇔ x 1 = 0 x 2 = a 2 < a < 3 (nhìn hình để xác định a).
f
'
u
=
0
⇔
u
=
x
1
u
=
x
2
⇔
f
x
=
x
1
=
0
f
x
=
x
2
=
a
2
<
a
<
3
f
x
=
0
⇔
x
∈
b
;
1
;
c
=
x
3
;
x
4
;
x
5
f x = a (nhìn vào đồ thị thể hiện bên ta thấy đồ thị hàm số f x cắt đường thẳng y = a (với 2 < a < 3 ) tại ba điểm phân biệt do vậy phương trình f x = a có ba nghiệm phân biệt x 6 ; x 7 ; x 8 .
Rõ ràng x 1 ,..., x 8 là đôi một khác nhau.
Kết hợp lại thì phương trình g ' x = 0 có 8 nghiệm phân biệt.
Đáp án B
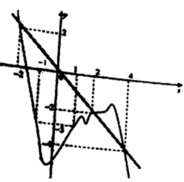
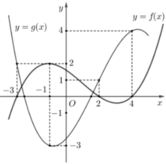
Phương pháp: Lập bảng biến thiên của g(x) và đánh giá số giao điểm của đồ thị hàm số y = g(x) và trục hoành.
Cách giải: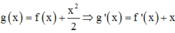 
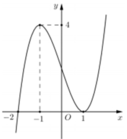
Xét giao điểm của đồ thị hàm sốy = f’(x) và đường thẳng y = -x ta thấy, hai đồ thị cắt nhau tại ba điểm có hoành độ là: -2;2;4 tương ứng với 3 điểm cực trị của y = g(x).
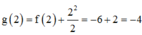
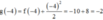
Bảng biến thiên:
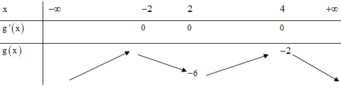
Dựa vào bảng biến thiên ta thấy 
=> phương trình g(x) = 0 không có nghiệm 
Với hàm số y=f(-2x+1) có
Với hàm số y=g(ax+b) có
y'=a.g'(ax+b)>0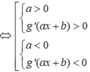 
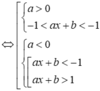
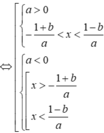
Vì hai hàm số đã cho có cùng khoảng đồng biến nên rơi vào trường hợp
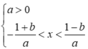và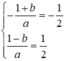 
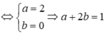
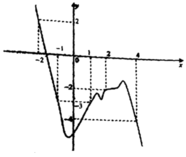
*Chú ý đồ thị đi lên hàm số đồng biến; đồ thị đi xuống hàm số nghịch biến.
Chọn đáp án C.
Đáp án C.
Ta có 
∀
x
∈
R
Khi đó 
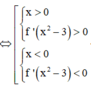
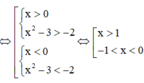
Suy ra hàm số đồng biến trên khoảng (–1;0) và (1;+ ∞)
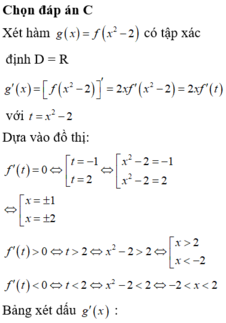
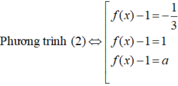
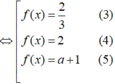
Đáp án B