



Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


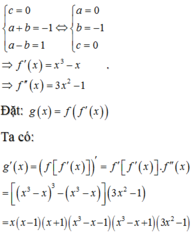



Chọn A
Ta có: g(x) = f(x-2017) - 2018x + 2019.
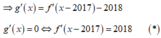
Nhận xét: tịnh tiến đồ thị hàm số y = f'(x) sang bên phải theo phương của trục hoành 2017 đơn vị ta được đồ thị hàm số y = f'(x-2017) . Do đó, số nghiệm của phương trình f'(x) = 2018 bằng số nghiệm của phương trình (*).
Dựa vào đồ thị ta thấy phương trình (*) có nghiệm đơn duy nhất hay hàm số đã cho có duy nhất 1 điểm cực trị.

Chọn A.
![]()
![]()
Giải phương trình g ' x = 0
![]()
Từ đồ thị hàm số y = f ' x
ta có f ' x = - 1
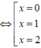
Ta có BBT của hàm g (x)

Từ BBT ta thấy hàm số g (x) đạt cực tiểu tại x = 1.

Chọn C.
Ta có f'(x)= 0
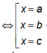
(Trong đó -2 < a < 0 < b < c < 2)
![]()
Ta có bảng xét dấuDựa vào bảng xét dấu ta thấy hàm số y = f(x) có 3 cực trị.

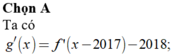
![]()
Dựa vào đồ thị hàm số y= f’(x) suy ra phương trình f’( x- 2017) = 2018 có 1 nghiệm đơn duy nhất.
Suy ra hàm số y= g( x) có 1 điểm cực trị

Đáp án B
Ta có
![]() .
.
![]() .
.
Hình bên dưới là đồ thị của hàm số ![]() và
và ![]() .
.
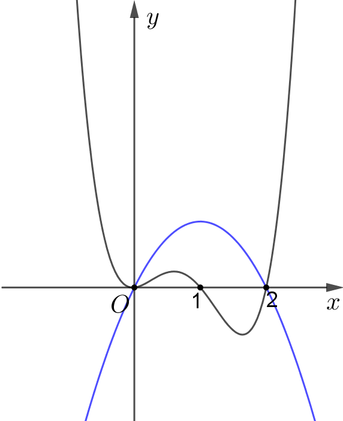
Dựa vào hình vẽ ta thấy đồ thị hàm số ![]() và
và ![]() cắt nhau tại 2 điểm phân biệt, đồng thời
cắt nhau tại 2 điểm phân biệt, đồng thời ![]() khi
khi ![]() hoặc
hoặc ![]() ,
, ![]() khi
khi ![]() .
.
Do đó ![]() đổi dấu qua
đổi dấu qua ![]() ,
, ![]() .
.
Vậy hàm số g(x) có hai điểm cực trị.

Ta có: f' (x - 2) = f' (x).(x-2)' = f'(x)
Do đó; đồ thị hàm số y= f’ (x) có hình dạng tương tự như trên.
Đồ thị hàm số y= f( x-2) có 3 điểm cực trị khi và chỉ khi đồ thị hàm số y= f( x) cũng có 3 điểm cực trị.
Chọn D.

Chọn B
+ Dựa vào đồ thị hàm số ta thấy :
- Hàm số y= f( x) nghịch biến trên khoảng ( - ∞; 1) và ( 3; 5) .
- Hàm số y= f( x) nghịch biến trên khoảng ( 1 ; 3) và ( 5 ; + ∞)
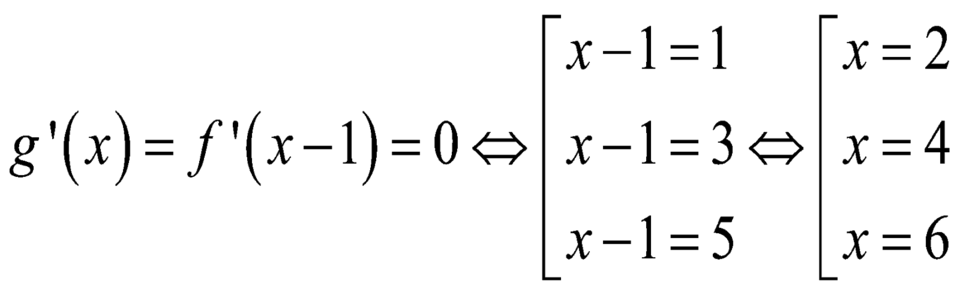
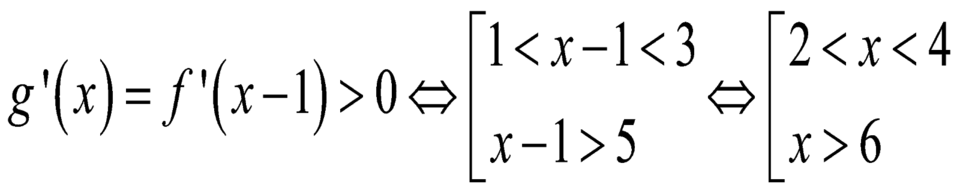

Chọn B
Ta có: ![]() .
.
Khi đó ![]() .
.
Vẽ đồ thị hàm số ![]() trên mặt phẳng toạ độ đã có đồ thị y= f’(x).
trên mặt phẳng toạ độ đã có đồ thị y= f’(x).
Dựa vào hình vẽ trên ta thấy phương trình ![]() có ba nghiệm đơn:
có ba nghiệm đơn:
x1< x2< x3
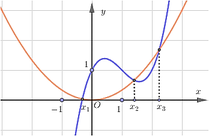
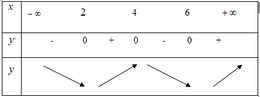
Ta lập được bẳng xét dấu của g’(x) :

Dựa vào bảng xét dấu ta thấy dấu của ![]() thay đổi từ
thay đổi từ ![]() sang
sang ![]() hai lần. Vậy có hai điểm cực tiểu.
hai lần. Vậy có hai điểm cực tiểu.

Chọn B
+ Với x= - 1: ta có : f’ (-1) = 0
Giá trị của hàm số y= f’(x) đổi dấu từ âm sang dương khi qua x= -1
=> Hàm số y= f(x) đạt cực tiểu tại điểm x= -1
+ Tại điểm x=0 hoặc x= 2
- Đạo hàm tại 2 điểm đó bằng 0.
- Giá trị của hàm số y= f’(x) không đổi dấu khi đi qua điểm đó. Nên x= 0; x= 2 không là điểm cực trị của hàm số