Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là C
f ' x = 0 ⇔ x x - 1 2 x + 1 = 0 ⇔ x = 0 x = 1 x = - 1
Nhận thấy x=1 là nghiệm bội chẵn nên f’(x) không đổi dấu qua x=1 do đó x=1 không phải là điểm cực trị của hàm số.
Nhận thấy x=0; x=-1 là các nghiệm bội lẻ nên f’(x) sẽ đổi dấu qua x=0; x=-1.
Vậy hàm số có 2 điểm cực trị

Đáp án D.
Ta có thể lập bảng xét dấu của f'(x) tuy nhiên thì ta có thể dùng mẹo như sau. Tại x=0; x=-2 thì y' đổi dấu do có mũ la lẻ còn x=1 thì không đổi dấu do mũ là chẵn. Vì vậy ta có thể có 2 cực trị.

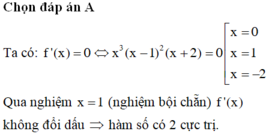



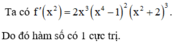
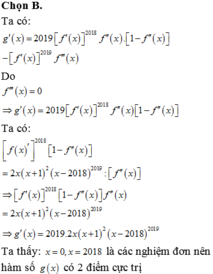
Đáp án D
f ' x đổi dấu khi đi qua điểm x = 1 , suy ra y = f x có 1 điểm cực trị.