Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Để y>0 thì x-7<0
hay x<7
b: Để y<0 thì x-7>0
hay x>7

Đồ thị hàm số đi qua O (0; 0)
Cho x = 2 ⇒ y = 1,5. 2 = 3
Ta có: A(2; 3)
Vẽ đường thẳng OA ta có đồ thị hàm số.
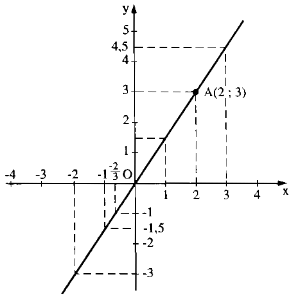
a) f(1) = 1,5. 1 = 1,5
f(-1) = 1,5. (-1) = -1,5
f(-2) = 1,5. (-2) = -3
f(2) = 1,5. 2 = 3
f(0) =0
b)\(y=-1\Rightarrow x=\dfrac{-1}{1,5}=-\dfrac{2}{3}\)
\(y=0\Rightarrow x=\dfrac{0}{1,5}=0\)
\(y=4,5\Rightarrow x=\dfrac{4,5}{1,5}=3\)
c) y > 0 ⇒1,5x > 0 ⇒x > 0
y < 0 ⇒ 1,5x < 0 ⇒ x < 0
Đồ thị hàm số đi qua O (0; 0)
Cho x = 2 ⇒⇒ y = 1,5. 2 = 3
Ta có: A(2; 3)
Vẽ đường thẳng OA ta có đồ thị hàm số.

a) f(1) = 1,5. 1 = 1,5
f(-1) = 1,5. (-1) = -1,5
f(-2) = 1,5. (-2) = -3
f(2) = 1,5. 2 = 3
f(0) = 0
b)y=−1⇒x=\(\dfrac{-1}{1,5}=-\dfrac{2}{3}\)
b)y=0⇒x==\(\dfrac{0}{1,5}=0\)
y=4,5⇒x=\(\dfrac{4,5}{1,5}=3\)
c) y > 0 ⇒1,5x > 0 ⇒x > 0
y < 0 ⇒ 1,5x < 0 ⇒ x < 0

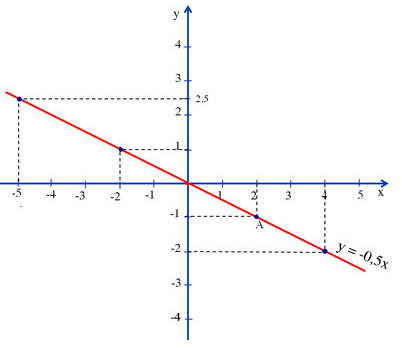
Cho x =2 được y =-2 =>A(2 ;-1) thuộc đồ thị. Vẽ đồ thị
a) Trên đồ thị ta thấy
f(2)=-1
f(-2) =1
f(4)=-2
f(0)=0;
b) Trên đồ thị ta thấy
y=-1 => x=2
y=0 => x=0
y=2,5 => x=-5
c) Khi y dương y > 0 ứng với phần đồ thị nằm trên trục hoành và bên trái trục tung nên x < 0.
Khi y âm : y < 0 ứng với phần đồ thị nằm trên trục hoành và bên phải trục tung nên x > 0

a) 2x + y – 1 = 0 => 2x + y = 1 có vô số giá trị
Các cặp giá trị có dạng (x∈ R; y = 1 – 2x)
Ví dụ: (x = 0; y =1); (x = 1; y = -1); ….
b) x – y – 3 => x – y = 3 có vô só giá trị
Các cặp giá trị có dạng (x∈ R; y = x – 3)
Ví dụ: (x = 0; y = -3); (x = 1; y = -2); ….
a) 2x + y - 1 = 0
giả sử nếu x = 3 thì ta có
2*3 + y - 1 =0
6-y+1=0
7-y=0
y=7
Vậy x=3 thì y = 7
b) x - y -3 = 0
Gỉa sử x = 4 thì ta có
4 - y - 3 = 0
1 - y = 0
y = 1
Vậy nếu x = 4 thì y = 1

\(1.\frac{x-7}{2}< 0\)
\(\Leftrightarrow\frac{x-7}{2}.2< 0.2\)
\(\Leftrightarrow x-7< 0\Leftrightarrow x< 7\)
\(S=\left\{xlx< 7\right\}\)
2)\(\)Đề biểu thức sau nhân giá trị âm thì :
\(\frac{x+3}{x-5}< 0\Leftrightarrow x+3< 0\Leftrightarrow x< 3\left(Đk:x\ne5\right)\)
\(S=\left\{xlx< 3\right\}\)
3.Giá trị của x thuộc Z để biểu thức sau nhận giá trị dương:
\(x^2+x\ge0\)
\(\Leftrightarrow x\left(x+1\right)\ge0\)
\(\Leftrightarrow\orbr{\begin{cases}x\ge0\\x+1\ge0\end{cases}\Leftrightarrow\orbr{\begin{cases}x\ge0\\x\ge-1\end{cases}}}\)
\(S=\left\{xlx\ge-1\right\}\)

1) Ta có : \(\frac{2016a+b+c+d}{a}=\frac{a+2016b+c+d}{b}=\frac{a+b+2016c+d}{c}=\frac{a+b+c+2016d}{d}\)
Trừ 4 vế với 2015 ta được : \(\frac{a+b+c+d}{a}=\frac{a+b+c+d}{b}=\frac{a+b+c+d}{c}=\frac{a+b+c+d}{d}\)
Nếu a + b + c + d = 0
=> a + b = -(c + d)
=> b + c = (-a + d)
=> c + d = -(a + b)
=> d + a = (-b + c)
Khi đó M = (-1) + (-1) + (-1) + (-1) = - 4
Nếu a + b + c + d\(\ne0\Rightarrow\frac{1}{a}=\frac{1}{b}=\frac{1}{c}=\frac{1}{d}\Rightarrow a=b=c=d\)
Khi đó M = 1 + 1 + 1 + 1 = 4
2) a) Ta có : \(\hept{\begin{cases}\left|x+2013\right|\ge0\forall x\\\left(3x-7\right)^{2004}\ge0\forall y\end{cases}\Rightarrow\left|x+2013\right|+\left(3x-7\right)^{2014}\ge0}\)
Dấu "=" xảy ra \(\hept{\begin{cases}x+2013=0\\3y-7=0\end{cases}\Rightarrow\hept{\begin{cases}x=-2013\\y=\frac{7}{3}\end{cases}}}\)
b) 72x + 72x + 3 = 344
=> 72x + 72x.73 = 344
=> 72x.(1 + 73) = 344
=> 72x = 1
=> 72x = 70
=> 2x = 0 => x = 0
c) Ta có :
\(\frac{7}{2x+2}=\frac{3}{2y-4}=\frac{5}{x+4}\Leftrightarrow\frac{7}{2x+2}=\frac{3}{2y-4}=\frac{10}{2x+8}=\frac{7-10}{2x+2-2x-8}=\frac{1}{2}\)(dãy tỉ số bằng nhau)
=> 2x + 2 = 14 => x = 6 ;
2y - 4 = 6 => y = 5 ;
6 + 5 + z = 17 => z = 6
Vậy x = 6 ; y = 5 ; z = 6
3) a) Ta có : \(\frac{a+b+c}{a+b-c}=\frac{a-b+c}{a-b-c}=\frac{a+b+c-a+b-c}{a+b-c-a+b+c}=\frac{2b}{2b}=1\)(dãy ti số bằng nhau)
=> a + b + c = a + b - c => a + b + c - a - b + c = 0 => 2c = 0 => c = 0;
Lại có : \(\frac{a+b+c}{a+b-c}-1=\frac{a-b+c}{a-b-c}-1\Leftrightarrow\frac{2c}{a+b-c}=\frac{2c}{a-b-c}\Rightarrow a+b-c=a-b-c\) => b = 0
Vậy c = 0 hoặc b = 0
c) Ta có : \(\frac{a+b}{c}=\frac{b+c}{a}=\frac{a+c}{b}=\frac{a+b+b+c+a+c}{c+a+b}=2\)(dãy tỉ số bằng nhau)
=> \(\hept{\begin{cases}a+b=2c\\b+c=2a\\a+c=2b\end{cases}}\)
Khi đó P = \(\left(1+\frac{c}{b}\right)\left(1+\frac{a}{c}\right)\left(1+\frac{b}{a}\right)=\frac{b+c}{b}.\frac{c+a}{c}=\frac{a+b}{a}=\frac{2a.2b.2c}{abc}=8\)
Vậy P = 8
2. b) \(7^{2x}+7^{2x+3}=344\)
\(7^{2x}\cdot\left(1+7^3\right)=344\)
\(7^{2x}\cdot\left(1+343\right)=344\)
\(7^{2x}\cdot344=344\)
\(7^{2x}=1\)
\(7^{2x}=7^0\)
\(2x=0\)
\(x=0\)
-Nếu y>0
=>-6.x>0
=>x<0
-Nếu y<0
=>-6.x<0
=>x>0
a) y = – 6x
y > 0 ⇒⇒ – 6x > 0 ⇒⇒ x < 0
Vậy mọi x ∈ R và x < 0 thì y = – 6x > 0.
b) y = – 6x
y < 0 ⇒⇒ -6x < 0 ⇒⇒ x > 0
Vậy x > 0 thì y = – 6x < 0.(x ∈ R)