Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -2 suy ra điểm A(0; -2) thuộc đồ thị hàm số hay -2 = 2.0 + m + 1 suy ra m = -3
Chọn A.

Câu 1 :
\(y=-\left(m^2+1\right)x+m-4\)
Để hàm số nghịch biến trên R
⇔ a < 0
⇔ \(-\left(m^2+1\right)\)< 0
⇔ \(m^2+1\) > 0
⇔ \(m^2\) > -1 ∀x ∈ R
⇔ m ∈ R
Vậy với mọi giá trị của m thì hàm số nghịch biến trên R
Câu 2 :
Gọi (d) : y =ax+b
Vì (d) cắt trục hoành tại điểm x = 3
nên (d) sẽ cắt điểm A(3;0)
A(3;0) ∈ (d) ⇔ 0 = 3a +b
Mà M(-2;4) ∈ (d) ⇔ 4 = -2a +b
Ta có : \(\left\{{}\begin{matrix}3a+b=0\\-2a+b=4\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}a=\dfrac{-4}{5}\\b=\dfrac{12}{5}\end{matrix}\right.\)
Vậy a=\(\dfrac{-4}{5}\) và b= \(\dfrac{12}{5}\)
Câu 3 :
(d) : \(y=2x+m+1\)
a) Vì (d) cắt trục hoành tại điểm có hoành độ bằng 3
nên (d) sẽ cắt điểm A(3;0)
A(3;0) ∈ (d) ⇔ 0 = 2 .3 + m+1⇔ m= -7
Vậy m = -7
b) Vì (d) cắt trục tung tại điểm có tung độ bằng -2
nên (d) sẽ cắt điểm B( 0;-2)
B( 0;-2) ∈ (d) ⇔ -2 = 0.2+m+1 ⇔ m = -3
Vậy m = -3

Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 3 suy ra điểm A(3; 0) thuộc đồ thị hàm số hay 0 = 2.3 + m + 1 suy ra m = -7
Chọn C.

a: Thay x=3 và y=0 vào (1), ta được:
\(6-3m=0\)
hay m=2

a: Khi m=1 thì (P): y=x^2+4x+1+1=x^2+4x+2
Thay y=-1 vào (P), ta được:
x^2+4x+2=-1
=>x^2+4x+3=0
=>(x+1)(x+3)=0
=>x=-1 hoặc x=-3
b: Phươngtrình hoành độ giao điểm là:
x^2+(2m+2)x+m^2+m=0
Δ=(2m+2)^2-4(m^2+m)
=4m^2+8m+4-4m^2-4m=4m+4
Để (P) cắt Ox tại hai điểm phân biệt thì 4m+4>0
=>m>-1
\(\left|x_1-x_2\right|=\sqrt{5}\)
=>\(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\sqrt{5}\)
=>(2m+2)^2-4(m^2+m)=5
=>4m^2+8m+4-4m^2-4m=5
=>4m+4=5
=>m=1/4

A) Để đồ thị đi qua điểm M(-1, 1) thì thay x = -1, y = 1 vào hàm số ta có:
1 = (2m-1).(-1) + m + 1
=> m = 1
B) Hàm số đã cho là hàm bậc nhất, đồ thị là đường thẳng nên không thể đồ thị cắt trục hoành tại hai điểm được
a)y=(2m-1)x+m+1
Đồ thị hàm số đi qua điểm M(-1;1) khi và chỉ khi
1=(2m-1)(-1)+m+1
Giải phương trình ẩn m, tìm được: m=1
b)y=(2m-1)x+m+1
Cho x=0⇒y=m+1⇒A(0; m+1 ) ⇒OA =\(\left|m+1\right|\)
Cho y =0 ⇒x =\(\frac{-m-1}{2m-1}\Rightarrow B\left(\frac{-m-1}{2m-1};0\right)\)
\(\Rightarrow OB=\left|\frac{-m-1}{2m-1}\right|=\frac{\left|m+1\right|}{\left|2m-1\right|}\)
△AOB cân ⇔\(\left\{{}\begin{matrix}OA=OB\\OA>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left|m+1\right|=\frac{\left|m+1\right|}{\left|2m-1\right|}\\\left|m+1\right|>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left|2m-1\right|=1\\m\ne-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2m-1=1\\2m-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=0\end{matrix}\right.\)
Vậy với m = 0 hoặc m = 1 thì đồ thị hàm số thỏa mãn yêu cầu của bài toán

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2-4x+1=2x-4\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-6x+5=0\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x-5\right)=0\\y=2x-4\end{matrix}\right.\)
\(\Leftrightarrow\left(x,y\right)\in\left\{\left(1;-2\right);\left(5;6\right)\right\}\)
c: Điểm M,N ở đâu vậy bạn?
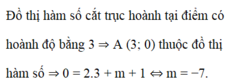
Đáp án A