PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 10 2020
m=2. Khi đó hàm số trở thành: f(x)= -4x-3
Khi đó hàm f(x) luôn nghịch biến vì hệ số a=-4<0
19 tháng 11 2021
Để hàm số đã cho đồng biến thì \(m^2-5m-6>0\)\(\Leftrightarrow m^2+m-6m-6>0\)\(\Leftrightarrow m\left(m+1\right)-6\left(m+1\right)>0\)\(\Leftrightarrow\left(m+1\right)\left(m-6\right)>0\)
Trường hợp 1: \(\hept{\begin{cases}m+1>0\\m-6>0\end{cases}}\Leftrightarrow\hept{\begin{cases}m>-1\\m>6\end{cases}}\Rightarrow m>6\)
Trường hợp 2: \(\hept{\begin{cases}m+1< 0\\m-6< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}m< -1\\m< 6\end{cases}}\Rightarrow m< -1\)
Vậy để hàm số đã cho đồng biến thì \(m>6\)hoặc \(m< -1\)
Để hàm số đã cho nghịch biến thì \(m^2-5m-6< 0\)\(\Leftrightarrow\left(m+1\right)\left(m-6\right)< 0\)
Trường hợp 1: \(\hept{\begin{cases}m+1< 0\\m-6>0\end{cases}}\Leftrightarrow\hept{\begin{cases}m< -1\\m>6\end{cases}}\)(loại vì m không thể vừa nhỏ hơn -1 lại vừa lớn hơn 6)
Trường hợp 2: \(\hept{\begin{cases}m+1>0\\m-6< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}m>-1\\m< 6\end{cases}}\Rightarrow-1< m< 6\)
Vậy để hàm số đã cho nghịch biến thì \(-1< m< 6\)
2 tháng 5 2017
a, \(\left\{{}\begin{matrix}m\ge0\\\sqrt{m}\ne\sqrt{5}\Leftrightarrow m\ne5\end{matrix}\right.\)
b, Để là hàm số đồng biến thì:\(\dfrac{\sqrt{m}+\sqrt{5}}{\sqrt{m}-\sqrt{5}}>0\Rightarrow\sqrt{m}+\sqrt{5}>0\Leftrightarrow m>5\)
LH
22 tháng 4 2017
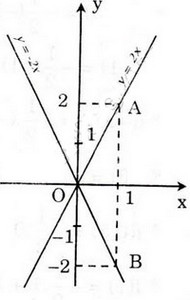
a) Trên mặt phẳng tọa độ Oxy. Với hàm số y = 2x cho x = 1 ta được y = 2, điểm A(1; 2) thuộc đồ thị y = 2x. Với hàm số y = -2x cho x = 1 ta được y = -2, điểm B(1; -2) thuộc đồ thị hàm số y = -2x, nên đường thẳng OB là đồ thị của hàm số y = -2x.
b) Ta có O(x1 = 0, y1 = 0) và A(x2 = 1, y2 = 2) thuộc đồ thị hàm số y = 2x, nên với x1 < x2 ta được f(x1) < f(x2).
Vậy hàm số y = 2x đồng biến trên R.
Lại có O(x1 = 0, y1 = 0) và B(x3 = 1, y3 = -2) thuộc đồ thị hàm số y = -2x, nên với x1 < x3 ta được f(x1) < f(x3).
Vậy hàm số y = -2x nghịch biến trên R.
22 tháng 4 2017
a) Đồ thị củahàm số y = 2x là đường thẳng đi qua O và điểm A(1; 2).
Đồ thị của hàm số y = -2x là đường thẳng đi qua O và điểm B(1; -2).
b) Hàm số y = 2x đồng biến vì khi x tăng lên thì y tương ứng tăng lên.
Hàm số y = -2x nghịch biến vì khi x tăng lên thì y tương ứng giảm đi.
| y = 2x | -1 | 0 | 1 | 2 |
| y = -2x | -2 | 0 | 2 | 4 |
| y = -2x | 2 | 0 | -2 | -4 |
Hàm số y = 2 + 3 2 − 3 + 2 − 3 2 + 3 x − 5 có:
a = 2 + 3 2 − 3 + 2 − 3 2 + 3 = 2 + 3 2 + 2 − 3 2 2 − 3 2 + 3 = 4 + 4 3 + 3 + 4 − 4 3 + 3 4 − 3 = 14 > 0
nên là hàm số đồng biến trên
Đáp án cần chọn là: B