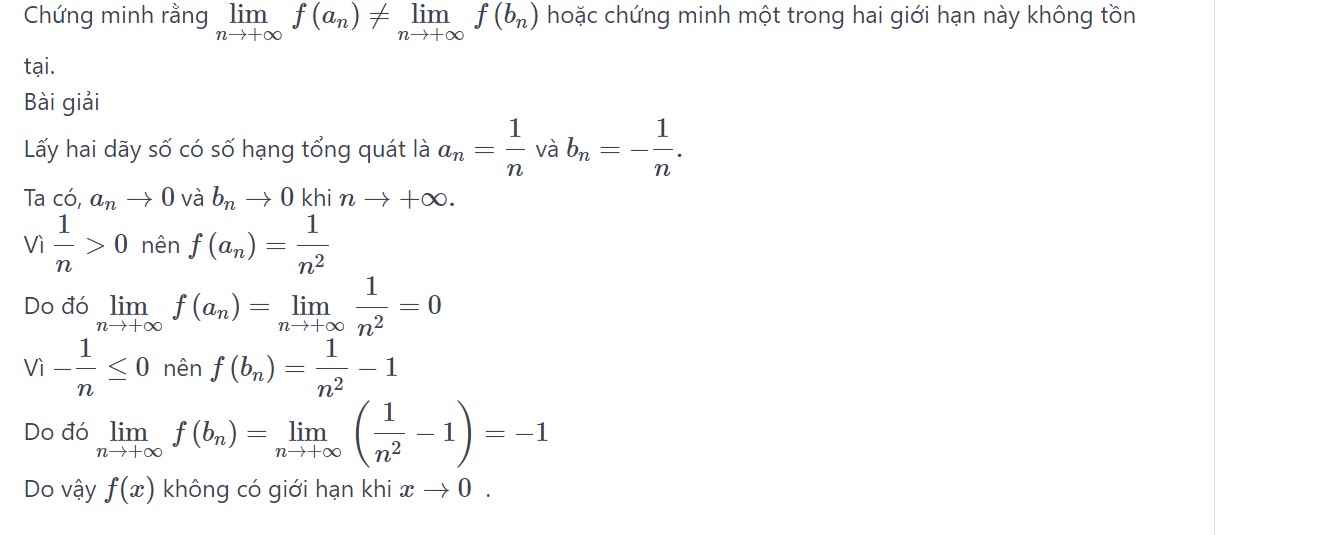Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f^3\left(2-x\right)-2f^2\left(2+3x\right)+x^2g\left(x\right)+36x=0\) (1)
Thay \(x=0\Rightarrow f^3\left(2\right)-2f^2\left(2\right)=0\Rightarrow\left[{}\begin{matrix}f\left(2\right)=0\\f\left(2\right)=2\end{matrix}\right.\)
Đạo hàm 2 vế của (1):
\(\Rightarrow-3f^2\left(2-x\right).f'\left(2-x\right)-12f\left(2+3x\right).f'\left(2+3x\right)+2x.g\left(x\right)+x^2.g'\left(x\right)+36=0\)
Thay \(x=0\)
\(\Rightarrow-3f^2\left(2\right).f'\left(2\right)-12f\left(2\right).f'\left(2\right)+36=0\)
TH1: \(f\left(2\right)=0\Rightarrow36=0\) (ktm)
TH2: \(f\left(2\right)=2\)
\(\Rightarrow-3.2^2.f'\left(2\right)-12.2.f'\left(2\right)+36=0\Rightarrow f'\left(2\right)=1\)
\(\Rightarrow A=3.2+4.1=10\)

\(\lim\limits_{x\rightarrow0}\left|f\left(x\right)\right|=\lim\limits_{x\rightarrow0}\left|x^2sin\dfrac{1}{x}\right|< \lim\limits_{x\rightarrow0}\left|x^2\right|=0\).
Vậy \(\lim\limits_{x\rightarrow0}f\left(x\right)=0\).
\(f\left(0\right)=A\).
Để hàm số liên tục tại \(x=0\) thì \(\lim\limits_{x\rightarrow0}f\left(x\right)=f\left(0\right)\Leftrightarrow A=0\).
Để xét hàm số có đạo hàm tại \(x=0\) ta xét giới hạn:
\(\lim\limits_{x\rightarrow0}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0}\dfrac{x^2sin\dfrac{1}{x}}{x}=\lim\limits_{x\rightarrow0}xsin\dfrac{1}{x}=0\).
Vậy hàm số có đạo hàm tại \(x=0\).

Ta xét bảng sau đây :
x 1 2 x-1 2 x-2 f(x) 1-x 4-2x 5-3x x-1 4-2x 3-x x-1 2x-4 3x-5
Ta có ngay với \(x\ne1\) và \(x\ne2\)
\(f'\left(x\right)=\begin{cases}-3;x< 1\\-1;1< x< 2\\3;x>2\end{cases}\)
Bây giờ xét tại \(x=1\), ta có
\(\lim\limits_{\Delta x\rightarrow0^+}\frac{f\left(1+\Delta x\right)-f\left(1\right)}{\Delta x}=\lim\limits_{\Delta x\rightarrow0^+}\frac{3-\left(1+\Delta x\right)-2}{\Delta x}=\lim\limits_{\Delta x\rightarrow0^+}\frac{-\Delta x}{\Delta x}=-1\)
\(\lim\limits_{\Delta x\rightarrow0^-}\frac{f\left(1+\Delta x\right)-f\left(1\right)}{\Delta x}\ne\lim\limits_{\Delta x\rightarrow0^-}\frac{5-3\left(1+\Delta x\right)-2}{\Delta x}=\lim\limits_{\Delta x\rightarrow0^-}\frac{-3\Delta x}{\Delta x}=-3\)
Như vậy \(\lim\limits_{\Delta x\rightarrow0^+}\frac{f\left(1+\Delta x\right)-f\left(1\right)}{\Delta x}\ne\lim\limits_{\Delta x\rightarrow0^-}\frac{f\left(1+\Delta x\right)-f\left(1\right)}{\Delta x}\)
Nghĩa là không tồn tại đạo hàm của \(f\left(x\right)\) tại \(x=1\)
Tương tự không tồn tại đạo hàm của \(f\left(x\right)\) tại \(x=2\)

Tham khảo:
Xét hàm số g(x) = f(x) − f(x + 0,5)
Ta có
g(0) = f(0) − f(0 + 0,5) = f(0) − f(0,5)
g(0,5) = f(0,5) − f(0,5 + 0,5) = f(0,5) − f(1) = f(0,5) − f(0)
(vì theo giả thiết f(0) = f(1)).
Do đó,


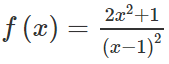 thì f(x) thỏa mãn được tất cả các điều kiện đã nêu
thì f(x) thỏa mãn được tất cả các điều kiện đã nêu