Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì 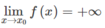
nên với dãy số ( x n ) bất kì, x n ∈ K \ x 0 và x n → x 0 ta luôn có
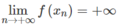
Từ định nghĩa suy ra f ( x n ) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì f ( x n ) > 1 kể từ một số hạng nàođó trởđi.
Nói cách khác, luôn tồn tạiít nhất một số x k ∈ K \ x 0 sao cho f ( x k ) > 1 .

Đáp án D
Cho hàm số f(x) xác định trên khoảng K chứa a. Hàm số f(x) liên tục tại x=a nếu ![]()

Chọn B.
Hàm số có nghĩa khi 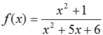 .
.
Vậy theo định lí ta có hàm số 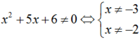 liên tục trên khoảng (-∞; -3); (-3; -2) và (-2; +∞).
liên tục trên khoảng (-∞; -3); (-3; -2) và (-2; +∞).

Trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\), \(f\left( x \right) = \frac{{{x^2} - 2x}}{x}\) là hàm phân thức hữu tỉ nên liên tục trên từng khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
Ta có: \(f\left( 0 \right) = a\)
\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \frac{{{x^2} - 2x}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{x\left( {x - 2} \right)}}{x} = \mathop {\lim }\limits_{x \to 0} \left( {x - 2} \right) = 0 - 2 = - 2\)
Để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) thì hàm số \(y = f\left( x \right)\) phải liên tục tại điểm \({x_0} = 0\). Khi đó:
\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right) \Leftrightarrow a = - 2\).
Vậy với \(a = - 2\) thì hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
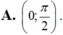
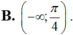
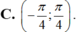
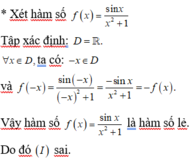
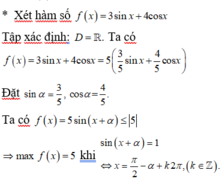



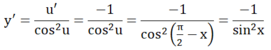
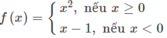
Chọn A.
TXĐ: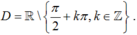 .
.
Với x = 0 ta có f(0) = 0.
Vậy hàm số gián đoạn tại x = 0.