Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(f'\left(x\right)=x^2-2x-3\)
\(f'\left(x\right)\le0\\ \Rightarrow x^2-2x-3\le0\\ \Leftrightarrow\left(x+1\right)\left(x-3\right)\le0\\ \Leftrightarrow-1\le x\le3\)

\(f'\left(x\right)=x^2+x+1\) luôn lớn hơn 0 mà :3 vậy f'(x) \(\le\)0 là k có :3
f'(x)= tính thế nào? hay là tính sai
nếu đúng vậy chọn PA (A) rỗng

2: ĐKXĐ: x<>1
\(f'\left(x\right)=\dfrac{\left(x^2-3x+3\right)'\left(x-1\right)-\left(x^2-3x+3\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=\dfrac{\left(2x-3\right)\left(x-1\right)-\left(x^2-3x+3\right)}{\left(x-1\right)^2}\)
\(=\dfrac{2x^2-5x+3-x^2+3x-3}{\left(x-1\right)^2}=\dfrac{x^2-2x}{\left(x-1\right)^2}\)
f'(x)=0
=>x^2-2x=0
=>x(x-2)=0
=>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
1:
\(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}\cdot x^2+8x-1\)
=>\(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2-2\sqrt{2}\cdot2x+8=x^2-4\sqrt{2}\cdot x+8=\left(x-2\sqrt{2}\right)^2\)
f'(x)=0
=>\(\left(x-2\sqrt{2}\right)^2=0\)
=>\(x-2\sqrt{2}=0\)
=>\(x=2\sqrt{2}\)

\(f'\left(x\right)=\left(x^2e^{-2x}\right)'=2x\cdot e^{-2x}-2x^2e^{-2x}\\ f'\left(x\right)=0\\ \Rightarrow2xe^{-2x}-2x^2e^{-2x}=0\\ \Leftrightarrow2xe^{-2x}\cdot\left(1-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)

Đáp án C.
- Phương pháp:
+) Tính f'(x).
+) Sử dụng quy tắc trong trái ngoài cùng giải bất phương trình bậc hai.
- Cách giải:
+ Ta có:
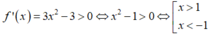
→ Vậy tập nghiệm của bất phương trình là 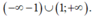

Chọn C.
Vì: f’(x) = 15(x + 1)2 + 4 ;
f”(x) = 30(x + 1) ⇔ f”(x) = 0 ⇔ x = -1.

Đáp án C
Ta có : f ' ( x ) = 15 ( x + 1 ) 2 + 4 ;
f ' ' ( x ) = 30 ( x + 1 ) ⇒ f ' ' ( x ) = 0 ⇔ 30 ( x + 1 ) = 0 ⇔ x = - 1 .

Ta có:
\(f'\left(x\right)=6x^2-2x\\ g'\left(x\right)=3x^2+x\)
Theo đề bài, ta có:
\(f'\left(x\right)>g'\left(x\right)\\ \Leftrightarrow6x^2-2x>3x^2+x\\ \Leftrightarrow3x^2-3x>0\\ \Leftrightarrow3x\left(x-1\right)>0\\ \Leftrightarrow\left[{}\begin{matrix}x>1\\x< 0\end{matrix}\right.\)
Vậy tập nghiệm của bất phương trình là \(\left(-\infty;0\right)\cup\left(1;+\infty\right)\)
Chọn D.
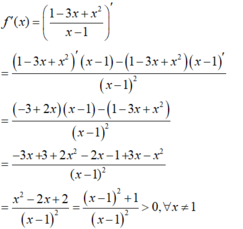
Chọn A
- Ta có:
- Suy ra bất phương trình vô nghiệm.