Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Phương trình hoành độ giao điểm là:
2x+4=-x+1
=>2x+x=1-4
=>3x=-3
=>x=-1
Thay x=-1 vào y=-x+1, ta được:
y=-(-1)+1=2
Vậy: A(-1;2)
b: A(-1;-2); B(-1;4); O(0;0)
\(OA=\sqrt{\left(-1-0\right)^2+\left(-2-0\right)^2}=\sqrt{1+4}=\sqrt{5}\)
\(OB=\sqrt{\left(-1-0\right)^2+4^2}=\sqrt{16+1}=\sqrt{17}\)
\(AB=\sqrt{\left(-1+1\right)^2+\left(4+2\right)^2}=6\)
Xét ΔOAB có \(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=\dfrac{5+17-36}{2\cdot\sqrt{5}\cdot\sqrt{17}}=\dfrac{-7}{\sqrt{85}}\)
=>\(sinAOB=\sqrt{1-\left(-\dfrac{7}{\sqrt{85}}\right)^2}=\dfrac{6}{\sqrt{85}}\)
Diện tích tam giác OAB là:
\(S_{AOB}=\dfrac{1}{2}\cdot AO\cdot OB\cdot sinAOB\)
\(=\dfrac{1}{2}\cdot\dfrac{6}{\sqrt{85}}\cdot\sqrt{17}\cdot\sqrt{5}=3\)

a, HS Tự làm
b, Tìm được C(–2; –3) là tọa độ giao điểm của d 1 và d 2
c, Kẻ OH ⊥ AB (CH ⊥ Ox)
S A B C = 1 2 C H . A B = 9 4 (đvdt)

Bài 1:
b: Thay y=0 vào (d2), ta được:
4x+1=0
hay \(x=-\dfrac{1}{4}\)
Vậy: \(A\left(-\dfrac{1}{4};0\right)\)
Thay x=0 vào (d2), ta được:
\(y=4\cdot0+1=1\)
Vậy: B(0;1)

a: Phương trình hoành độ giao điểm là:
3x-4=4x-6
\(\Leftrightarrow3x-4x=-6+4\)
\(\Leftrightarrow-x=-2\)
hay x=2
Thay x=2 vào \(\left(d1\right)\), ta được:
\(y=3\cdot2-4=2\)
b: Thay y=0 vào \(\left(d1\right)\), ta được:
\(3x-4=0\)
hay \(x=\dfrac{4}{3}\)
Thay x=0 vào \(\left(d1\right)\), ta được:
\(y=3\cdot0-4=-4\)
Vậy: \(A\left(\dfrac{4}{3};0\right);B\left(0;-4\right)\)

a: Tọa độ A là:
y=0 và -1/2x+4=0
=>x=8 và y=0
=>A(8;0)
Tọa độ B là;
y=0 và -x+4=0
=>x=4 và y=0
=>B(4;0)
Tọa độ C là;
1/2x+4=-x+4 và y=-x+4
=>x=0 và y=4
=>C(0;4)
b: A(8;0); B(4;0); C(0;4)
\(AB=\sqrt{\left(4-8\right)^2+\left(0-0\right)^2}=4\)
\(AC=\sqrt{\left(0-8\right)^2+\left(4-0\right)^2}=4\sqrt{5}\)
\(BC=\sqrt{4^2+4^2}=4\sqrt{2}\)
\(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{2}{\sqrt{5}}\)
=>\(sinBAC=\dfrac{1}{\sqrt{5}}\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC=\dfrac{1}{2}\cdot4\cdot4\sqrt{5}\cdot\dfrac{1}{\sqrt{5}}=8\)
\(C=4+4\sqrt{5}+4\sqrt{2}\)

b: Tọa độ điểm A là:
\(\left\{{}\begin{matrix}3x=-x+4\\y=3x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)

1) \(\left\{{}\begin{matrix}\left(d_1\right):y=2x\\\left(d_2\right):y=-\dfrac{1}{2}x+5\end{matrix}\right.\)
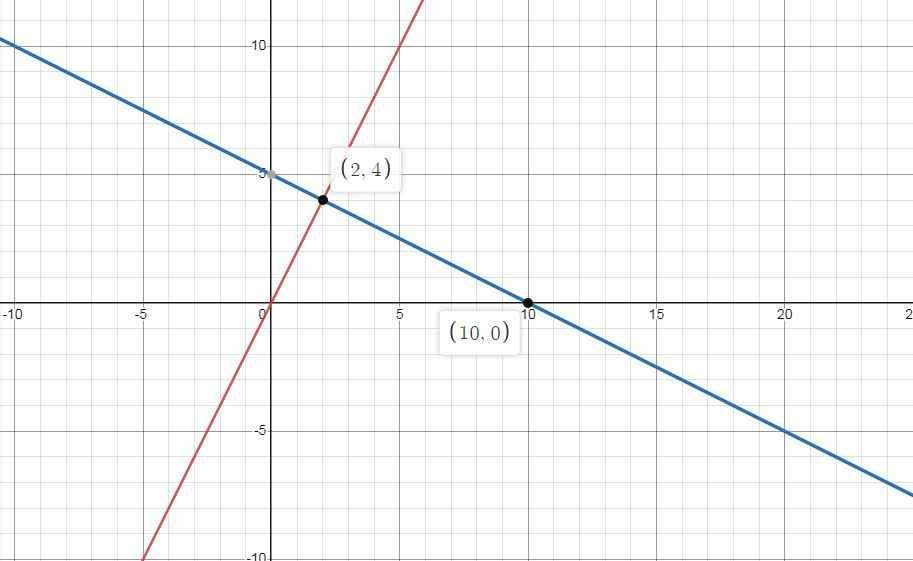
2) Theo đồ thi ta có :
\(\left(d_1\right)\cap\left(d_2\right)=A\left(2;4\right)\)
3) \(\left(d_2\right)\cap Ox=B\left(a;0\right)\)
\(\Leftrightarrow-\dfrac{1}{2}a+5=0\)
\(\Leftrightarrow\dfrac{1}{2}a=5\)
\(\Leftrightarrow a=10\)
\(\Rightarrow\left(d_2\right)\cap Ox=B\left(10;0\right)\)
4) \(OA=\sqrt[]{\left(2-0\right)^2+\left(4-0\right)^2}=\sqrt[]{20}=2\sqrt[]{5}\)
\(OB=\sqrt[]{\left(10-0\right)^2+\left(0-0\right)^2}=\sqrt[]{10^2}=10\)
\(AB=\sqrt[]{\left(10-2\right)^2+\left(0-4\right)^2}=\sqrt[]{80}=4\sqrt[]{5}\)
Ta thấy :
\(OA^2+AB^2=20+80=OB^2=100\)
\(\Rightarrow\Delta OAB\) vuông tại A
\(\Rightarrow\widehat{OAB}=90^o\)
\(sin\widehat{AOB}=\dfrac{AB}{OB}=\dfrac{4\sqrt[]{5}}{10}=\dfrac{2\sqrt[]{5}}{5}\)
\(\Rightarrow\widehat{AOB}\sim63,43^o\)
\(\Rightarrow\widehat{OBA}=90^o-63,43^o=26,57^o\)
5) Chu vi \(\Delta OAB\) :
\(AB+OA+OB=4\sqrt[]{5}+2\sqrt[]{5}+10=10\sqrt[]{5}+10=10\left(\sqrt[]{5}+1\right)\left(đvmd\right)\)
Diện tích \(\Delta OAB\) :
\(\dfrac{1}{2}AB.OA=\dfrac{1}{2}.4\sqrt[]{5}.2\sqrt[]{5}=20\left(đvdt\right)\)

b) Phương trình hoành độ giao điểm của (D1) và (d2) là:
-x+4=x-4
\(\Leftrightarrow-2x=-8\)
hay x=4
Thay x=4 vào (d1), ta được:
y=-4+4=0
Thay x=0 vào (d1), ta được:
\(y=-0+4=4\)
Thay x=0 vào (d2), ta được:
\(y=0-4=-4\)
Vậy: A(0;4); B(0;-4); C(4;0)
1: Tọa độ A là:
\(\left\{{}\begin{matrix}2x+4=-x+1\\y=-x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=-3\\y=-x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-\left(-1\right)+1=2\end{matrix}\right.\)
vậy: A(-1;2)
2: O(0;0); A(-1;2); B(-1;-4)
\(OA=\sqrt{\left(-1-0\right)^2+\left(2-0\right)^2}=\sqrt{5}\)
\(OB=\sqrt{\left(-1-0\right)^2+\left(-4-0\right)^2}=\sqrt{17}\)
\(AB=\sqrt{\left(-1+1\right)^2+\left(-4-2\right)^2}=6\)
Xét ΔOAB có \(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=\dfrac{5+17-36}{2\cdot\sqrt{5}\cdot\sqrt{17}}=-\dfrac{7}{\sqrt{85}}\)
=>\(sinAOB=\sqrt{1-\left(-\dfrac{7}{\sqrt{85}}\right)^2}=\dfrac{6}{\sqrt{85}}\)
Diện tích tam giác AOB là:
\(S_{AOB}=\dfrac{1}{2}\cdot OA\cdot OB\cdot sinAOB\)
\(=\dfrac{1}{2}\cdot\dfrac{6}{\sqrt{85}}\cdot\sqrt{5}\cdot\sqrt{17}=3\)