Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

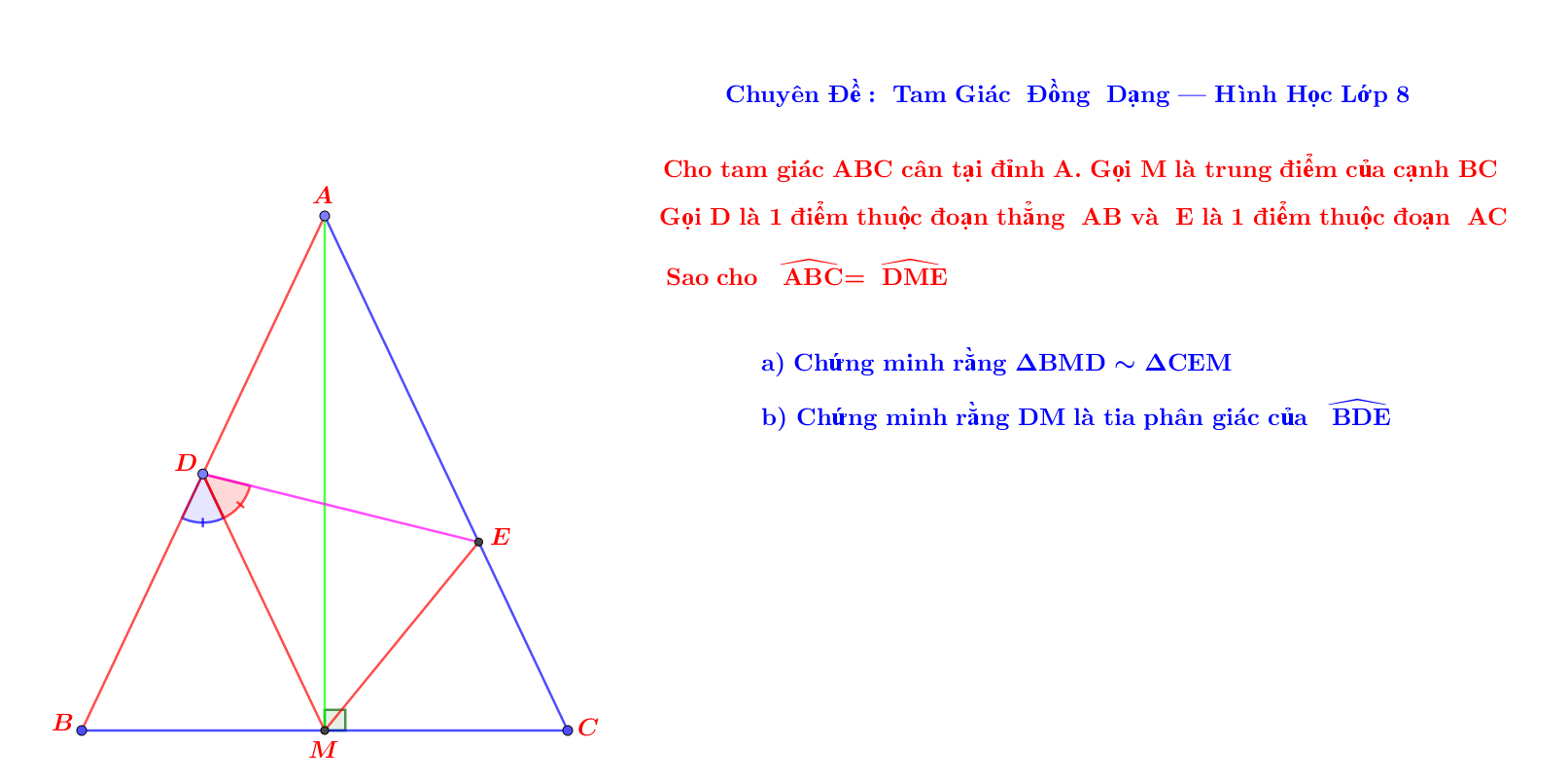
a) \(\widehat{BDM}=180^0-\widehat{BMD}-\widehat{DBM}=180^0-\widehat{BMD}-\widehat{DME}=\widehat{CME}\)
\(\Rightarrow\)△BMD∼△CEM (g-g)
b) \(\Rightarrow\dfrac{BD}{CM}=\dfrac{MD}{EM}\Rightarrow\dfrac{BD}{BM}=\dfrac{MD}{EM}\)
\(\Rightarrow\)△BMD∼△MED (c-g-c).
\(\Rightarrow\widehat{BDM}=\widehat{MDE}\Rightarrow\)DM là tia p/g góc BDE.

Xét tam giác A’B’C’ và tam giác ABC có:
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) và \(\widehat {A'} = \widehat A = 90^\circ \)
\( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\) (c-g-c)

Ta thấy
\(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{2}{6} = \frac{1}{3}\\\frac{{AC}}{{A'C'}} = \frac{3}{9} = \frac{1}{3}\\ \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\end{array}\)
Xét tam giác ABC và tam giác A’B’C’ có:
\(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\) và \(\widehat A = \widehat {A'}\)
\( \Rightarrow \Delta ABC \backsim \Delta A'B'C'\) (c-g-c)
\( \Rightarrow \)\(\widehat B = \widehat {B'},\,\,\widehat C = \widehat {C'}\)

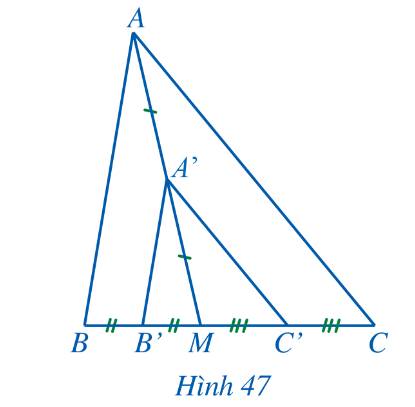
a) Xét tam giác ABM có A'B' là đường trung bình của tam giác
\( \Rightarrow A'B' // AB\)
\( \Rightarrow \widehat {C'B'A'} = \widehat {CBA}\) (hai góc đồng vị)
Tương tự, tam giác AMC có A'C' là đường trung bình nên \( = \widehat {ACB}\) (hai góc đồng vị)
Xét tam giác ABC có:
\( \widehat {BAC} + \widehat {CBA} + \widehat {ACB} = 180^0\)
Xét tam giác A'B'C' có:
\( \widehat {B'A'C'} + \widehat {C'B'A'} + \widehat {A'C'B'} = 180^0\)
\(\Rightarrow \widehat {BAC} + \widehat {CBA} + \widehat {ACB} = \widehat {B'A'C'} + \widehat {C'B'A'} + \widehat {A'C'B'}\)
\(\Rightarrow \widehat {BAC} = \widehat {B'A'C'}\)
b) A'B' là đường trung bình của tam giác ABM nên
\(A'B' = \frac {1}{2} AB \Rightarrow \frac {A'B'}{AB} = \frac {1}{2}\)
A'B' là đường trung bình của tam giác ABM nên
\(A'C' = \frac {1}{2} AC \Rightarrow \frac {A'C'}{AC} = \frac {1}{2}\)
Ta có: \( \frac{B'C'}{BC} = \frac{MB' +MC'}{2MB' + 2MC'} = \frac{MB' +MC'}{2(MB' + MC')} = \frac{1}{2}\)
\( \Rightarrow \frac{A'B'}{AB} = \frac{B'C'}{BC} = \frac{C'A'}{CA} \)

\(\dfrac{B'A}{B'C}=\dfrac{S_{AMB'}}{S_{CMB'}}=\dfrac{S_{ABB'}}{S_{CBB'}}=\dfrac{S_{ABB'}-S_{AMB'}}{S_{CBB'}-S_{CMB'}}=\dfrac{S_{ABM}}{S_{CBM}}\)
\(\dfrac{C'A}{C'B}=\dfrac{S_{AMC'}}{S_{BMC'}}=\dfrac{S_{ACC'}}{S_{BCC'}}=\dfrac{S_{ACC'}-S_{AMC'}}{S_{BCC'}-S_{BMC'}}=\dfrac{S_{ACM}}{S_{CBM}}\)
\(\dfrac{MA}{MA'}=\dfrac{S_{ABM}}{S_{A'BM}}=\dfrac{S_{ACM}}{S_{A'CM}}=\dfrac{S_{ABM}+S_{ACM}}{S_{A'BM}+S_{A'CM}}=\dfrac{S_{ABM}+S_{ACM}}{S_{MBC}}=\dfrac{S_{ABM}}{S_{MBC}}+\dfrac{S_{ACM}}{S_{MBC}}=\dfrac{B'A}{B'C}+\dfrac{C'A}{C'B}\)

Vì \(MN\parallel B'C'\) nên \(\widehat {A'MN} = \widehat {A'B'C'}\) (hai góc đồng vị)
\( \Rightarrow \widehat M = \widehat B\)
Xét tam giác A’MN và tam giác ABC có:
\(\widehat {A'} = \widehat A;\,\,A'M = AB;\,\,\widehat M = \widehat B\)
\( \Rightarrow \Delta A'MN = \Delta ABC\) (g-c-g)
Vì \(MN\parallel B'C'\) nên \(\Delta A'MN \backsim \Delta A'BC\)
\( \Rightarrow \Delta ABC \backsim \Delta A'BC\)

Lời giải:
a) Ta thấy:
$\frac{4}{8}=\frac{5}{10}=\frac{6}{12}$ nên 2 tam giác đồng dạng theo TH c.c.c
b) Pitago: $A'C'=\sqrt{B'C'^2-A'B'^2}=\sqrt{16^2-9^2}=5\sqrt{7}$
Xét tam giác $ABC$ và $A'B'C'$ có:
$\widehat{A}=\widehat{A'}=90^0$
$\frac{AB}{AC}\neq \frac{A'B'}{A'C'}$
Do đó 2 tam giác không đồng dạng
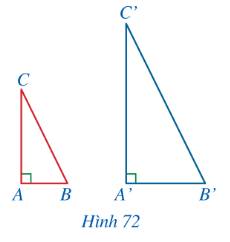

Ta có: \(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}} \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\)
Hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ nên \(\widehat {A'} = \widehat A = 90^\circ \).
Xét tam giác ABC và tam giác A’B’C’ có:
\(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\) và \(\widehat {A'} = \widehat A\)
\( \Rightarrow \Delta ABC \backsim \Delta A'B'C'\) (c-g-c)
\( \Rightarrow \widehat B = \widehat {B'}\).