Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
\(A\cup B=(-2;2)\)
\(A\cap B=\left\{0\right\}\)
\(A\setminus B=(-2;0)\)
Về hình vẽ trên trục số thì đơn giản rồi. Bạn có thể tự vẽ.

\(A\cup B=\left(-2;2\right)\)
\(A\cap B=0\)
A\B=(-2;0)

\(A\cup B=\left(-2;2\right)\)
\(A\cap B=\left\{0\right\}\)
\(A\B=\left(-2;0\right)\)

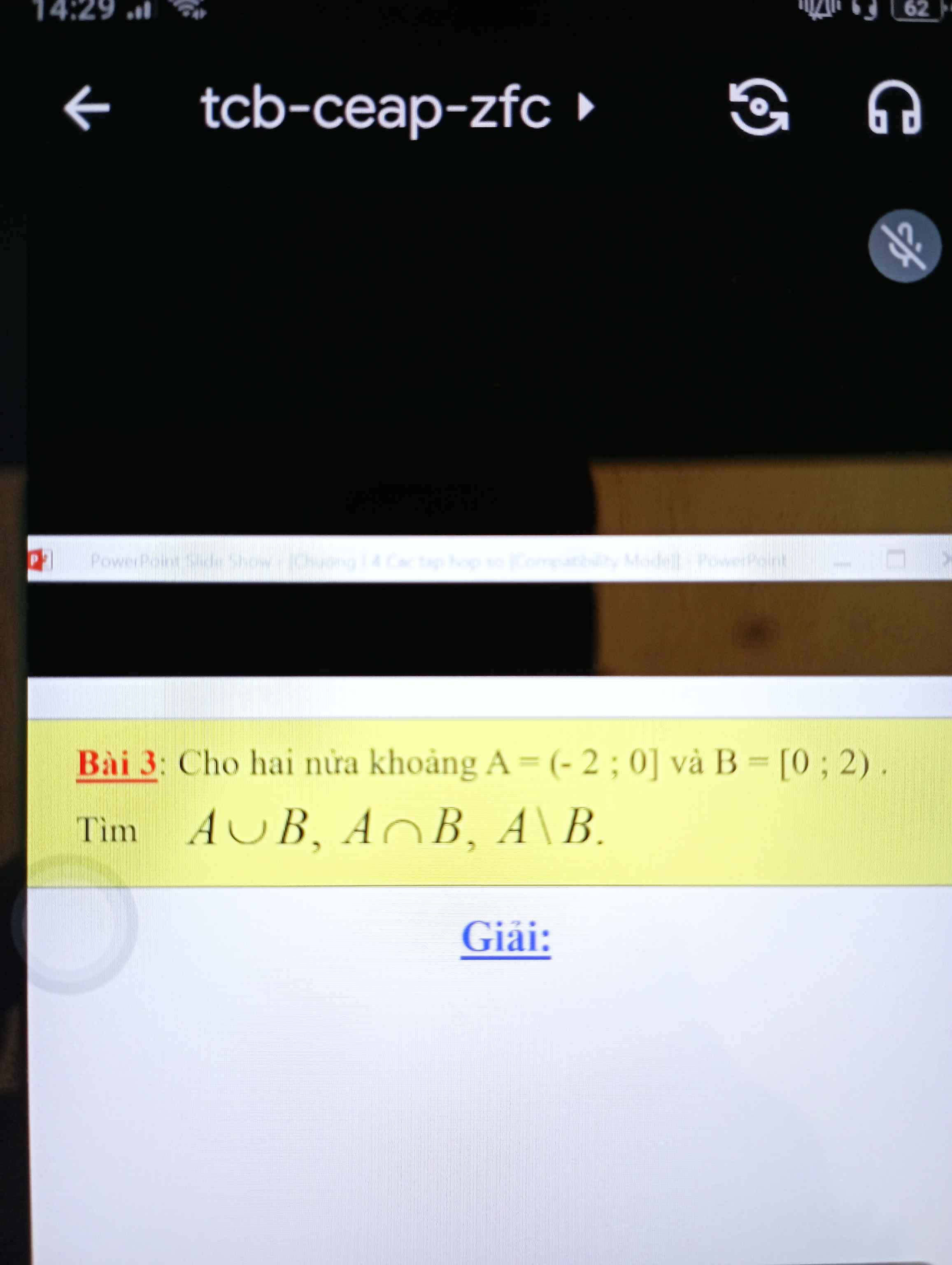
Trong mặt phẳng Oxy, cho hai điểm A(2;0) và B(6;4). Viết phương trình đường tròn (C) tiếp xúc với trục hoành tại A và khoảng cách từ tâm của (C) đến B bằng 5.
Gọi I(a;b) là tâm của đường tròn (C).
*) Vì đường tròn tiếp xúc với trục hoành tại A(2; 0) nên I(2;b) và R = b.
Phương trình đường tròn (C) có dạng: (x-2 ) 2 + (y-b ) 2 = b 2
*) Khoảng cách từ B(6;4) đến tâm I(2;b) bằng 5 nên ta có:
IB = 5 ⇒ 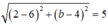
⇒ (2 - 6 ) 2 + (b - 4 ) 2 = 25
⇒ 16 + (b - 4 ) 2 = 25
⇒ (b - 4 ) 2 = 9
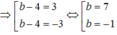
+) Với b = 7, phương trình đường tròn (C) là (x - 2 ) 2 + (y - 7 ) 2 = 49
+) Với b = 1, phương trình đường tròn (C) là (x - 2 ) 2 + (y + 1 ) 2 = 1
Vậy phương trình đường tròn (C) là (x - 2 ) 2 + (y - 7 ) 2 = 49 hoặc (x - 2 ) 2 + (y + 1 ) 2 = 1.

\(A=[4;+\infty)\)
\(B=\left(6;9\right)\)
\(B\backslash A=\varnothing\)

Trong mặt phẳng Oxy, cho hai điểm A(2;0) và B(6;4). Viết phương trình đường tròn (C) tiếp xúc với trục hoành tại A và khoảng cách từ tâm của (C) đến B bằng 5.
Gọi I(a;b) là tâm của đường tròn (C).
Vì đường tròn tiếp xúc với trục hoành tại A(2; 0) nên I(2;b) và R = b.
Phương trình đường tròn (C) có dạng: \(\left(x-2\right)^2+\left(y-b\right)^2=b^2\)
Trong mặt phẳng Oxy, cho hai điểm A(2;0) và B(6;4). Viết phương trình đường tròn (C) tiếp xúc với trục hoành tại A và khoảng cách từ tâm của (C) đến B bằng 5.
Gọi I(a;b) là tâm của đường tròn (C).
Vì đường tròn tiếp xúc với trục hoành tại A(2; 0) nên I(2;b) và R = b.
Khoảng cách từ B(6;4) đến tâm I(2;b) bằng 5 nên ta có:
\(IB=5\Rightarrow\sqrt{\left(2-6\right)^2+\left(b-4\right)^2}=5\)
\(\Rightarrow\left(2-6\right)^2+\left(b-4\right)^2=25\)
\(\Rightarrow16+\left(b-4\right)^2=25\)
\(\Rightarrow\left(b-4\right)^2=9\)
\(\Leftrightarrow\left[{}\begin{matrix}b-4=3\\b-4=-3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}b=7\\b=-1\end{matrix}\right.\)
Với b = 7, phương trình đường tròn (C) là \(\left(x-2\right)^2+\left(y-7\right)^2=49\)
Với b = 1, phương trình đường tròn (C) là \(\left(x-2\right)^2+\left(y-2\right)^2=1\)
Vậy phương trình đường tròn (C) là \(\left(x-2\right)^2+\left(y-7\right)^2=49\) hoặc \(\left(x-2\right)^2+\left(y-2\right)^2=1\)
 . Từ đó suy ra hình dạng của tam giác ABC.
. Từ đó suy ra hình dạng của tam giác ABC.
\(A\cup B=\left(-2;2\right)\\ A\cap B=\left\{0\right\}\\ A\B=\left(-2;0\right)\)