Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

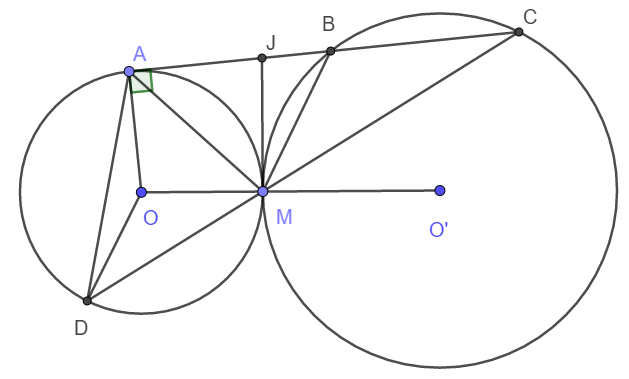
a) Từ M, kẻ \(MJ\perp OO'\left(J\in AC\right)\)
Khi đó ta có \(\widehat{BMA}=\widehat{BMJ}+\widehat{JMA}=\widehat{BCM}+\widehat{ADM}\)
\(=\frac{\widebat{AD}-\widebat{AM}}{2}+\frac{\widebat{AM}}{2}=\frac{\widebat{AD}}{2}=\widehat{AMD}\)
Vậy MA là tia phân giác góc \(\widehat{BMD}\)
b) Xét tam giác AMB và DMA có:
\(\widehat{BAM}=\widehat{ADM}\left(=\frac{\widebat{AM}}{2}\right)\)
\(\widehat{AMB}=\widehat{DMA}\left(cma\right)\)
\(\Rightarrow\Delta AMB\sim\Delta DMA\left(g-g\right)\)
\(\Rightarrow\frac{AM}{MD}=\frac{MB}{AM}\Rightarrow AM^2=MD.MB\)

a: OH*OM=OA^2=R^2
b: ΔOCD cân tại O
mà OI là đường trung tuyến
nên OI vuông góc với CD
Xét tứ giác OIAM có
góc OIM=góc OAM=90 độ
nên OIAM là tứ giác nội tiếp
c: Xét ΔOHK vuông tại H và ΔOIM vuông tại I có
góc HOK chung
Do đo: ΔOHK đồng dạng với ΔOIM
=>OH/OI=OK/OM
=>OI*OK=OH*OM=R^2=OC^2
mà CI vuông góc với OK
nên ΔOCK vuông tại C
=>KC là tiếp tuyến của (O)