Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Phương pháp:
Giải phương trình hoành độ giao điểm, tìm giao điểm của hai đồ thị.
Dựa vào công thức trọng tâm, xác định m.
Cách giải:
Phương trình hoành độ giao điểm của d và (C) là
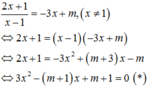
Để d cắt (C) tại hai điểm phân biệt A, B thì (*) có 2 nghiệm phân biệt khác 1
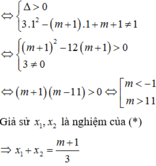


Đáp án C
Ta có ∆ : x = a + 5 t ' y = 1 - 12 t ' t ' ∈ ℝ z = - 5 - t ' ⇒ giải hệ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇔ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇒ a = 8

Đáp án A
Gọi ![]()
Ta có:
M
A
→
=
k
M
B
→
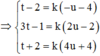
Giả hệ với ẩn t; k và ku 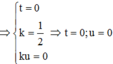
![]()

Đáp án B
Điểm N ∈ d ⇒ N - 2 + 2 t ; 1 + t ; 1 - t mà A là trung điểm của MN ⇒ M 4 - 2 t ; 5 - t ; 3 + t
Mặt khác M = ∆ ∩ P ⇒ M ∈ P ⇒ 2 4 - 2 t - 5 - t + 3 + t - 10 = 0 ⇔ t = - 2
Khi đó M ( 8 ; 7 ; 1 ) , N ( - 6 ; - 1 ; 3 ) ⇒ M N → = - 14 ; - 8 ; 2 ⇒ M N : x + 6 7 = y + 1 4 = z - 3 - 1 .






Chọn: D