Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mỗi bài, mk làm một phần ví dụ cho cậu nhé
nó đối xứng với nhau qua pt đường thẳng đenta,
trường hợp (d) ko cắt (đen ta) hay (d) cắt (đen ta) thì đều làm theo phương pháp sau
lấy 2 điểm bất kì thuộc (d) thì ta có như sau: A(0:1) là điểm thuộc đường thẳng (d)
lấy A' đối xứng với A qua (đen ta)
liên hệ tính chất đối xứng qua đường thẳng thì hiểu là AA' vuông góc (đen ta)
đồng thời giao điểm của AA' với (đen ta) là trung điểm của AA'
dễ dàng tìm đc giao điểm của (đen ta) với (d) là K(-2/5;1/5)
từ pt (đenta) thì dễ dàng =) vecto pháp tuyến của (đenta) =) (3;-4)
vì AA' vuông góc với (đenta) nên =) vectơ pháp tuyến của AA' là (4;-3)
áp véctơ pháp tuyến của AA' vào phương trình tổng quát đc: 4(x-0)-3(y-1)=0 (=) 4x-3y+3=0
gọi I là giao điểm của AA' và (đenta) =) I(-6/7;-1/7)
mà I là trung điểm của AA'
chắc chắn cậu sẽ dễ dàng suy ra điểm A'
mà K và A' thuộc (d') nên dễ dàng =) phương trình của (d')

4 câu làm tương tự nhau, nhưng câu a chắc bạn ghi nhầm đề (hoặc đề sai). Do \(AB\perp CC'\) nhưng \(4.2+1.2\ne0\) là hoàn toàn vô lý
Mình làm câu b, 2 câu còn lại bạn làm tương tự
Gọi H là trực tâm tam giác \(\Rightarrow\) H là giao điểm BB' và CC'
Tọa độ H là nghiệm \(\left\{{}\begin{matrix}4x-3y+1=0\\7x+2y-22=0\end{matrix}\right.\) \(\Rightarrow H\left(\frac{64}{29};\frac{95}{29}\right)\)
B là giao điểm BC và BB' nên tọa độ B là nghiệm:
\(\left\{{}\begin{matrix}5x-3y+2=0\\4x-3y+1=0\end{matrix}\right.\) \(\Rightarrow B\left(-1;-1\right)\)
C là giao điểm BC và CC' nên tọa độ C là nghiệm:
\(\left\{{}\begin{matrix}5x-3y+2=0\\7x+2y-22=0\end{matrix}\right.\) \(\Rightarrow C\left(2;4\right)\)
Đường AA' đi qua H và vuông góc BC nên nhận \(\left(3;5\right)\) là 1 vtpt
Phương trình AA':
\(3\left(x-\frac{64}{29}\right)+5\left(x-\frac{95}{29}\right)=0\Leftrightarrow3x+5y-23=0\)
Đường thẳng AB qua B và vuông góc CC' nên nhận \(\left(2;-7\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x+1\right)-7\left(y+1\right)=0\Leftrightarrow2x-7y-5=0\)
Đường thẳng AC qua C và vuông góc BB' nên nhận \(\left(3;4\right)\) là 1 vtpt
Phương trình AC:
\(3\left(x-2\right)+4\left(y-4\right)=0\Leftrightarrow3x+4y-22=0\)

Tọa độ A là:
2x-3y+12=0 và 2x+3y=0
=>x=-3 và y=2
Tọa độ M, M là trung điểm của BC là M(x;-3x/2)
Phương trình BC sẽ là: 3x+2y+c=0
Thay x=4 và y=-1 vào BC, ta được:
3*4+2*(-1)+c=0
=>c+12-2=0
=>c=-10
=>BC: 3x+2y-10=0
=>B(x;5-1,5x); y=5-1,5x
B(x;5-1,5x); C(4;-1); M(x;-3x/2)
Theo đề, ta có: x=(4+x)/2 và -1,5x=(5x-1)/2
=>2x=x+4 và -3x=5x-1
=>x=4 và -8x=-1(loại)
=>Không có điểm B nào thỏa mãn

Ta có \(AC\perp d\Rightarrow\overrightarrow{n_{AC}}.\overrightarrow{n_d}=0\) đường thẳng AC nhận \(\overrightarrow{n_{AC}}=\left(3;2\right)\) là một vecto pháp tuyến
\(\Rightarrow\) Phương trình đường thẳng AC:
\(3\left(x-4\right)+2\left(y+1\right)=0\Leftrightarrow3x+2y-10=0\)
Mà C là giao điểm của AC và \(d_1\Rightarrow\) tọa độ C là nghiệm của hệ:
\(\left\{{}\begin{matrix}2x+3y=0\\3x+2y-10=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=6\\y=-4\end{matrix}\right.\) \(\Rightarrow C\left(6;-4\right)\)
Gọi M là trung điểm AB \(\Rightarrow M\in d_1\Rightarrow M\left(a;\dfrac{-2a}{3}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_B=2x_M-x_A=2a-4\\y_B=2y_M-y_A=\dfrac{3-4a}{3}\end{matrix}\right.\) \(\Rightarrow B\left(2a-4;\dfrac{3-4a}{3}\right)\)
Mặt khác, do \(B\in d\Rightarrow2x_B-3y_B=0\)
\(\Rightarrow2\left(2a-4\right)-3\left(\dfrac{3-4a}{3}\right)=0\)
\(\Leftrightarrow8a-11=0\Rightarrow a=\dfrac{11}{8}\Rightarrow B\left(\dfrac{-5}{4};\dfrac{-5}{6}\right)\)

Bài 2:
Gọi đường cao và trung tuyến là BH và BM
Do B là giao điểm BH và BM nên tọa độ B là nghiệm:
\(\left\{{}\begin{matrix}2x-3y+12=0\\2x+3y=0\end{matrix}\right.\) \(\Rightarrow B\left(-3;2\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(-7;3\right)\Rightarrow\) đường thẳng AB nhận \(\left(3;7\right)\) là 1 vtpt
Phương trình AB:
\(3\left(x-4\right)+7\left(y+1\right)=0\Leftrightarrow3x+7y-5=0\)
Gọi \(C\left(a;b\right)\Rightarrow\overrightarrow{AC}=\left(a-4;b+1\right)\)
Do \(BH\perp AC\) mà BH nhận \(\left(2;-3\right)\) là 1 vtpt nên: \(\frac{a-4}{2}=\frac{b+1}{-3}\Leftrightarrow3a+2b=10\)
Gọi M là trung điểm AC \(\Rightarrow M\left(\frac{a+4}{2};\frac{b-1}{2}\right)\)
\(M\in BM\Rightarrow2\left(\frac{a+4}{2}\right)+3\left(\frac{b-1}{2}\right)=0\) \(\Leftrightarrow2a+3b=-5\)
\(\Rightarrow\left\{{}\begin{matrix}3a+2b=10\\2a+3b=-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=8\\b=-7\end{matrix}\right.\) \(\Rightarrow C\left(8;-7\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\left(4;-6\right)\\\overrightarrow{BC}=\left(11;-9\right)\end{matrix}\right.\)
Bạn tự viết nốt 2 pt đường thẳng AC và BC còn lại, các yếu tố có đủ rồi đấy
Bài 1:
Thay tọa độ A vào 2 pt đường thẳng thấy đều ko thỏa mãn
Vậy đó là 2 đường cao xuất phát từ B và C, giả sử chúng là BH: 9x-3y-4=0 và CK: x+y-2=0
Do \(AC\perp BH\) nên đường thẳng AC nhận \(\left(1;3\right)\) là 1 vtpt
Phương trình AC:
\(1\left(x-2\right)+3\left(y-2\right)=0\Leftrightarrow x+3y-8=0\)
Do \(AB\perp CK\) nên AB nhận \(\left(1;-1\right)\) là 1 vtpt
Phương trình AB:
\(1\left(x-2\right)-1\left(y-2\right)=0\Leftrightarrow x-y=0\)
B là giao điểm CH và AB nên tọa độ B là nghiệm: \(\left\{{}\begin{matrix}9x-3y-4=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow B\left(\frac{2}{3};\frac{2}{3}\right)\)
C là giao điểm AC và CK nên tọa độ C là nghiệm \(\left\{{}\begin{matrix}x+3y-8=0\\x+y-2=0\end{matrix}\right.\) \(\Rightarrow C\left(-1;3\right)\)
\(\Rightarrow\overrightarrow{BC}=\left(-\frac{5}{3};\frac{7}{3}\right)=\frac{1}{3}\left(-5;7\right)\)
Đường thẳng BC nhận \(\left(7;5\right)\) là 1 vtpt
Phương trình BC:
\(7\left(x+1\right)+5\left(y-3\right)=0\Leftrightarrow7x+5y-8=0\)

4 câu giống nhau, mình làm câu a, bạn tự làm 3 câu còn lại hoàn toàn tương tự:
a/ Đường thẳng d nhận \(\left(1;-2\right)\) là 1 vtpt
Gọi d' là đường thẳng qua M và vuông góc d \(\Rightarrow\) d' nhận \(\left(2;1\right)\) là 1 vtpt
Phương trình d':
\(2\left(x-4\right)+1\left(y-1\right)=0\Leftrightarrow2x+y-9=0\)
Gọi H là hình chiếu vuông góc của M lên d \(\Rightarrow\) H là giao điểm của d và d'
Tọa độ H là nghiệm: \(\left\{{}\begin{matrix}x-2y+4=0\\2x+y-9=0\end{matrix}\right.\) \(\Rightarrow H\left(\frac{14}{5};\frac{17}{5}\right)\)
Gọi M' là điểm đối xứng với M qua d \(\Rightarrow\) H là trung điểm MM'
Tọa độ M': \(\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=\frac{8}{5}\\y_{M'}=2y_H-y_M=\frac{29}{5}\end{matrix}\right.\) \(\Rightarrow M'\left(\frac{8}{5};\frac{29}{5}\right)\)

Bất phương trình bậc nhất 2 ẩn :
\(2x+3y>0\Rightarrow Câu\) \(C\)
\(x-2y\le1\Rightarrow Câu\) \(f\)
\(4\left(x-1\right)+5\left(y-3\right)>2x-9\)
\(\Leftrightarrow4x-4+5y-15-2x+9>0\)
\(\Leftrightarrow2x+5y-10>0\) \(\Rightarrow Câu\) \(i\)
Đáp án: A
M(3;2), N(-1;-4)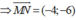
Gọi I là trung điểm của MN ⇒ I(1;-1)
Đường thẳng trung trực của MN là đường thẳng đi qua I và nhận vecto MN làm vecto pháp tuyến:
MN: -4(x - 1) - 6(y + 1) = 0 ⇔ 2x + 3y + 1 = 0