
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

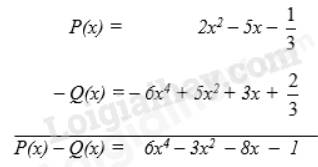

a: \(P\left(x\right)=-5x^4+2x^2-8x+\dfrac{1}{2}\)
\(Q\left(x\right)=4x^4+2x^3-5x^2-6x+\dfrac{3}{2}\)
b: \(A\left(x\right)=-5x^4+2x^2-8x+\dfrac{1}{2}+4x^4+2x^3-5x^2-6x+\dfrac{3}{2}=-x^4+2x^3-3x^2-14x+2\)
\(B\left(x\right)=-5x^4+2x^2-8x+\dfrac{1}{2}-4x^4-2x^3+5x^2+6x-\dfrac{3}{2}=-9x^4-2x^3+7x^2-2x-1\)

Theo cột dọc:
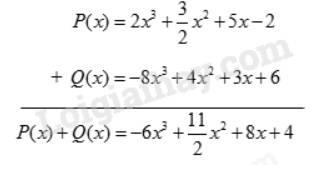
Theo hàng ngang:
\(\begin{array}{l}P(x) + Q(x) = 2{x^3} + \dfrac{3}{2}{x^2} + 5x - 2 + ( - 8){x^3} + 4{x^2} + 3x + 6\\ = (2 - 8){x^3} + (\dfrac{3}{2} + 4){x^2} + (5 + 3)x + ( - 2 + 6)\\ = - 6{x^3} + \dfrac{{11}}{2}{x^2} + 8x + 4\end{array}\)

a)A=\(x^5-\dfrac{1}{2}x+7x^3-2x+\dfrac{1}{5}x^3+3x^4-x^5+\dfrac{2}{5}x^4+15\)
=\(=\dfrac{-5}{2}x+\dfrac{36}{5}x^3+\dfrac{17}{5}x^4+15\)
b)B=\(3x^2-10+\dfrac{2}{5}x^3+7x-x^2+8+7x^2\)
\(=9x^2+\dfrac{2}{5}x^3+7x+2\)
c)C=\(\dfrac{1}{7}x-2x^4+5x+6\)

P(x)=-5x^3-1/3+8x^4+x^2
Q(x)=x^4-2x^3+x^2-5x-2/3
P(x)+Q(x)
=x^4-2x^3+x^2-5x-2/3+8x^4-5x^3+x^2-1/3
=9x^4-7x^3+2x^2-5x-1
P(x)-Q(x)
=x^4-2x^3+x^2-5x-2/3-8x^4+5x^3-x^2+1/3
=-7x^4+3x^3-5x-1/3

a) x5-3x2+x4-\(\dfrac{1}{2}\)x-x5+5x4+x2-1
= (x5-x5)+(x4+5x4)+(x2-3x2)-\(\dfrac{1}{2}\)x-1
= 6x4-2x2-\(\dfrac{1}{2}\)x-1
b) x-x9+x2-5x3+x6-x+3x9+2x6-x3+7
= (3x9-x9)+(2x6+x6)-(5x3+x3)+x2+(x-x)+7
= 2x9+3x6-6x3+x2+7

a: \(P\left(-1\right)=3-1+\dfrac{7}{4}=\dfrac{7}{4}+2=\dfrac{15}{4}\)
\(Q\left(\dfrac{1}{2}\right)=-3\cdot\dfrac{1}{4}+2\cdot\dfrac{1}{2}+2=-\dfrac{3}{4}+3=\dfrac{9}{4}\)
b: Đặt P(x)-Q(x)=0
\(\Leftrightarrow3x^2+x+\dfrac{7}{4}=-3x^2+2x+2\)
\(\Leftrightarrow6x^2-x-\dfrac{1}{4}=0\)
\(\Leftrightarrow24x^2-4x-1=0\)
\(\text{Δ}=\left(-4\right)^2-4\cdot24\cdot\left(-1\right)=112>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{4-4\sqrt{7}}{48}=\dfrac{1-\sqrt{7}}{12}\\x_2=\dfrac{1+\sqrt{7}}{12}\end{matrix}\right.\)

a) -P(x) đã được thu gọn và đã được sắp xếp theo lũy thừa giảm.
- Thu gọn: \(Q\left(x\right)=5x^4-x^5+x^2-2x^3+3x^2-\dfrac{1}{4}\)
\(Q\left(x\right)=5x^4-x^5+\left(x^2+3x^2\right)-2x^3-\dfrac{1}{4}\)
\(Q\left(x\right)=5x^4-x^5+4x^2-2x^3-\dfrac{1}{4}\)
-Sắp xếp: \(Q\left(x\right)=-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)
b)-Tính P(x)+Q(x)
\(P\left(x\right)+Q\left(x\right)=\left(x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x\right)+\left(-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\right)\)
\(P\left(x\right)+Q\left(x\right)=12x^4-11x^3+2x^2-\dfrac{1}{4}x-\dfrac{1}{4}\)
-Tính P(x)-Q(x)
\(P\left(x\right)-Q\left(x\right)=\left(x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x\right)-\left(-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\right)\)
\(P\left(x\right)-Q\left(x\right)=x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x+x^5-5x^4+2x^3-4x^2+\dfrac{1}{4}\)
\(P\left(x\right)-Q\left(x\right)=\left(x^5+x^5\right)+\left(7x^4-5x^4\right)-\left(9x^3-2x^3\right)-\left(2x^2+4x^2\right)-\dfrac{1}{4}x+\dfrac{1}{4}\)
\(P\left(x\right)-Q\left(x\right)=2x^5+2x^4-7x^3-6x^2-\dfrac{1}{4}x+\dfrac{1}{4}\)

Rút gọn :
\(P\left(x\right)=x^5-3x^2+7x^4-9x^3+x^2-\dfrac{1}{4}x\)
\(P\left(x\right)=x^5+\left(-3x^2+x^2\right)+7x^4-9x^3-\dfrac{1}{4}x\)
\(P\left(x\right)=x^5-2x^2+7x^4-9x^3-\dfrac{1}{4}x\)
\(Q\left(x\right)=5x^4-x^5+x^2-2x^3+3x^2-\dfrac{1}{4}\)
\(Q\left(x\right)=5x^4-x^5+\left(x^2+3x^2\right)-2x^3-\dfrac{1}{4}\)
\(Q\left(x\right)=5x^4-x^5+4x^2-2x^3-\dfrac{1}{4}\)
a) Sắp xếp : \(P\left(x\right)=x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x\)
\(Q\left(x\right)=-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)
b) SGK có hướng dẫn, mở ra là biết làm liền, phần này t lười :))
c) Thay x = 0 vào Q(x) với P(x) (mấy cái chỗ có chữ x ), tính ra thì kết luận "Vậy giá trị của biểu thức...khi thay x = 0 là..." . Nếu tính xong cả 2 biểu thức rồi thì ghi là "=> x = 0 không phải là nghiệm của đa thức Q(x)".
Thông cảm, lười quá độ :))