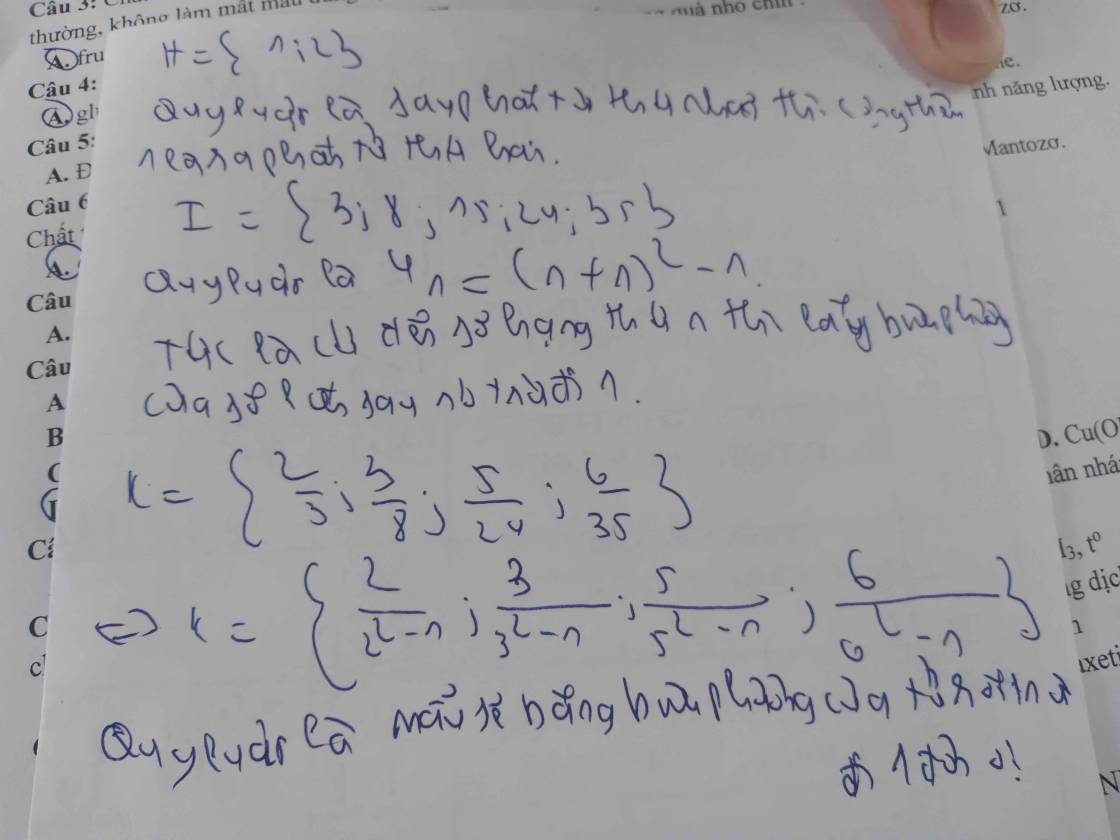
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
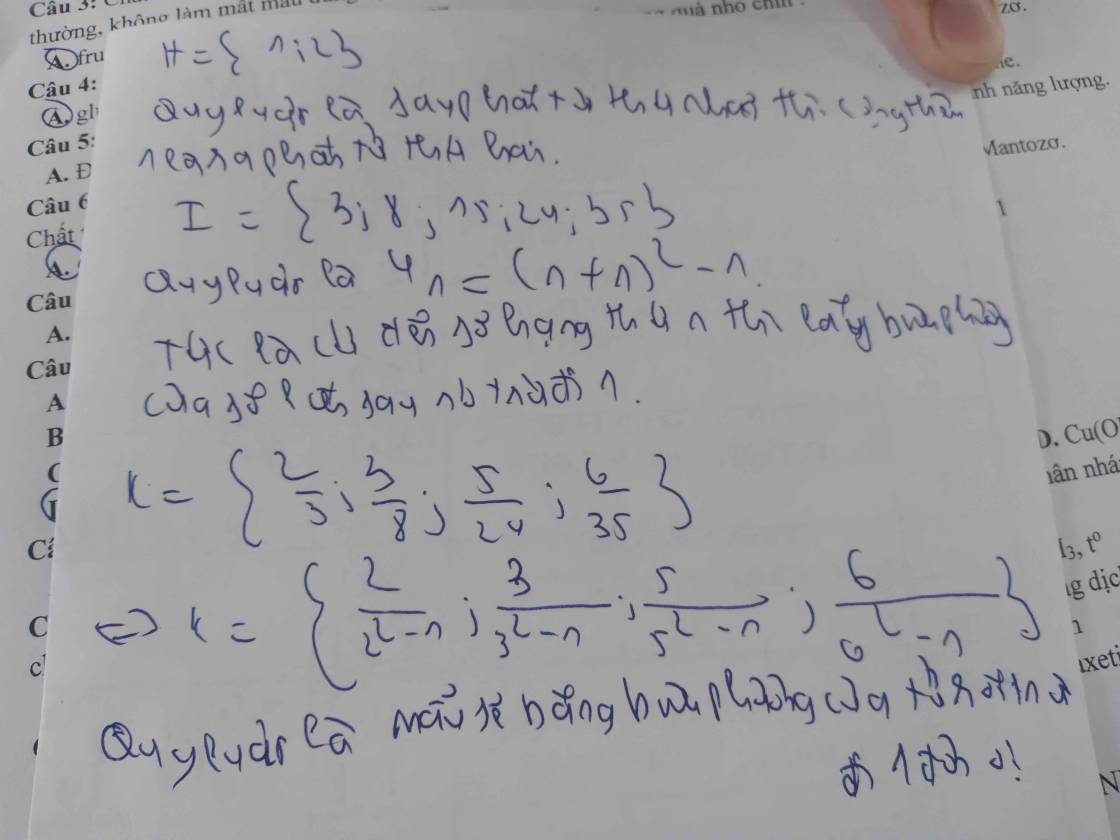
a) A = {\(\dfrac{1}{n\left(n+1\right)}\)| \(n\in\mathbb{N},1\le n\le5\)}
b) B = {\(\dfrac{1}{n^2-1}\)|\(n\in\mathbb{N},2\le n\le6\)\(\)}
a) \(A=\left\{x\in N|x=3k+1;0\le k\le3;k\in z\right\}\)
b) \(B=\left\{x\in Q^+|x=\dfrac{k}{k^2-1};2\le k\le6;k\in N\right\}\)
Ta có:
Tập hợp A:
\(A=\left[-5;\dfrac{1}{2}\right]\)
Tập hợp B:
\(B=\left(-3;+\infty\right)\)
Mà: \(A\cap B\)
\(\Rightarrow\left\{x\in R|-3\le x\le\dfrac{1}{2}\right\}\)
⇒ Chọn A
\(\Leftrightarrow\dfrac{x+1}{\left(x+1\right)^2-1}+\dfrac{x+6}{\left(x+6\right)^2-1}=\dfrac{x+2}{\left(x+2\right)^2-1}=\dfrac{x+5}{\left(x+5\right)^2-1}\)
\(\Leftrightarrow\left(x+1\right)\left(x+6\right)^2-x-1+\left(x+6\right)\left(x+1\right)^2-x-6=\left(x+2\right)\left(x+5\right)^2-x-2+\left(x+5\right)\left(x+2\right)^2-x-5\)
=>(x+1)(x+6)^2+(x+6)(x+1)^2=(x+2)(x+5)^2+(x+2)^2(x+5)
=>(x+1)(x+6)(x+6+x+1)=(x+2)(x+5)(x+5+x+2)
=>(2x+7)[x^2+7x+6-x^2-7x-10]=0
=>(2x+7)=0
=>x=-7/2
Bài 2:
a: \(A=11+\dfrac{3}{13}-2-\dfrac{4}{7}-5-\dfrac{3}{13}\)
\(=4-\dfrac{4}{7}=\dfrac{24}{7}\)
b: \(B=6+\dfrac{4}{9}+3+\dfrac{7}{11}-4-\dfrac{4}{9}\)
\(=5+\dfrac{7}{11}=\dfrac{62}{11}\)
c: \(C=\dfrac{-5}{7}\left(\dfrac{2}{11}+\dfrac{9}{11}\right)+1+\dfrac{5}{7}=1\)
d: \(D=\dfrac{7}{10}\cdot\dfrac{8}{3}\cdot20\cdot\dfrac{3}{8}\cdot\dfrac{5}{28}\)
\(=\dfrac{20}{10}\cdot7\cdot\dfrac{8}{3}\cdot\dfrac{3}{8}\cdot\dfrac{5}{28}=2\cdot\dfrac{5}{4}=\dfrac{5}{2}\)
\(\left(-\infty;\dfrac{1}{3}\right)\cap\left(\dfrac{1}{4};+\infty\right)=\left(\dfrac{1}{4};\dfrac{1}{3}\right)\)
\(\left(-\dfrac{11}{2};7\right)\cap\left(-2;\dfrac{27}{2}\right)=\left(-2;7\right)\)
\(\left(0;12\right)\cap[5;+\infty)=[5;12)\)
\(R\cap\left[-1;1\right]=\left[-1;1\right]\)
\(A=\left(-1,5\right)^2\cdot2\dfrac{2}{3}-\dfrac{1}{6}+\left(\dfrac{4}{7}-\dfrac{2}{5}\right):1\dfrac{1}{35}\)
\(=\left(-\dfrac{3}{2}\right)^2\cdot\dfrac{8}{3}-\dfrac{1}{6}+\left(\dfrac{20}{35}-\dfrac{14}{35}\right):\dfrac{36}{35}\\ =\dfrac{9}{4}\cdot\dfrac{8}{3}-\dfrac{1}{6}+\dfrac{6}{35}\cdot\dfrac{35}{36}\\ =6-\dfrac{1}{6}+\dfrac{1}{6}\\ =6\)
