Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cứ vẽ hình ra mới hiểu nha (tui k vẽ hình ở đây được)
Xét tam giác ohn và tam giác ohm ta có :
hn=hm(gt)
góc ohm= góc ohn (=90o)
oh: cạnh chung
=>tam giác ohm= tam giác ohn
=>on=om(hai cạnh tương ứng)
(Xem đây rồi tự chứng minh câu sau nhé)

x y O M I H A B
xét tam giác OMI và tam giác OAI có : OI chung
IM = IA (gt)
^OIM = ^OIA = 90
=> tam giác OMI = tam giác OAI (2cgv)
=> OM = OA (1)
xét tam giác OHM và tam giác OHB có : OH chung
HB = HM (gt)
^OHB = ^OHM = 90
=> tam giác OHM = tam giác OHB (2cgv)
=> OB = OM và (1)
=> OA = OB
Hình bạn tự kẻ nha , mình ghi bải giải
Xét tam giác OAM có : OI là đường cao(Vì OI vuông góc với AM )
OI là trung tuyến(Vì I là trung điểm AM)
=> Tam giác OAM cân tại O (vì có đường cao vừa là đường trung tuyến)
=> OA = OM (1)
Xét tam giác OBM có : OH là đường cao(Vì OH vuông góc với BM)
OH là trung tuyến(Vì H là trung điểm BM)
=> Tam giác OBM cân tại O(Vì có đường cao vừa là đường trung tuyến)
=> OM = OB (2)
Từ (1) và (2) suy ra OA = OB (vì cùng bằng OM)
Học Tốt

$3)$ Ta có:
\(\widehat{POQ}=\widehat{POM}+\widehat{MOQ}\\ =2\widehat{HOM}+2\widehat{KOM}\\ =2\left(\widehat{HOM}+\widehat{KOM}\right)\\ =2.\widehat{xOy}=2.60^o=120^o\)
a) Xét 2 \(\Delta\) vuông \(OHM\) và \(OHP\) có:
\(\widehat{OHM}=\widehat{OHP}=90^0\left(gt\right)\)
\(HM=HP\left(gt\right)\)
Cạnh OH chung
=> \(\Delta OHM=\Delta OHP\) (2 cạnh góc vuông tương ứng bằng nhau).
Xét 2 \(\Delta\) vuông \(OKM\) và \(OKQ\) có:
\(\widehat{OKM}=\widehat{OKQ}=90^0\left(gt\right)\)
\(KM=KQ\left(gt\right)\)
Cạnh OK chung
=> \(\Delta OKM=\Delta OKQ\) (2 cạnh góc vuông tương ứng bằng nhau).
b) Theo câu a) ta có \(\Delta OHM=\Delta OHP.\)
=> \(OM=OP\) (2 cạnh tương ứng) (1).
+ Theo câu a) ta có \(\Delta OKM=\Delta OKQ.\)
=> \(OM=OQ\) (2 cạnh tương ứng) (2).
Từ (1) và (2) => \(OP=OQ.\)
=> \(\Delta OPQ\) cân tại \(O\left(đpcm\right).\)
Mình làm câu a và b đó, câu c) bạn dưới làm rồi.
Chúc bạn học tốt!
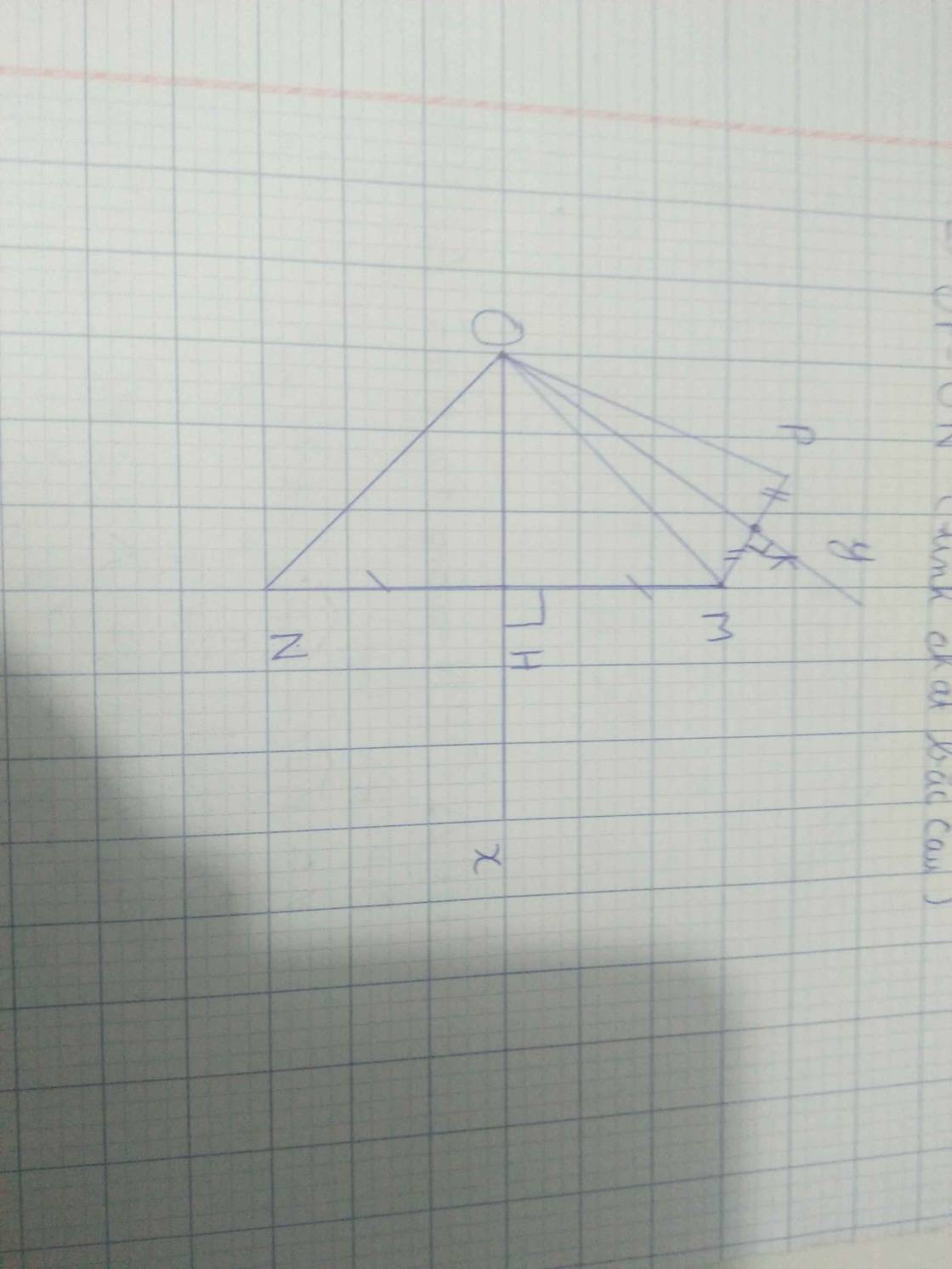


x y O M H K P Q
a) *Xét △OHP và △OHM có:
OH chung
∠OHP=∠OHM (=900)
HP=HM (gt)
⇒△OHP = △OHM (cgc)
*Xét △OKM và △OKQ có:
OK chung
∠OKM=∠OKQ (=900)
KM=KQ (gt)
⇒△OKM = △OKQ (cgc)
b)△OHP = △OHM⇒ OP=OM (2 cạnh tương ứng) (1)
△OKM = △OKQ⇒ OM=OQ (2 cạnh tương ứng) (2)
Từ (1) và (2) ⇒OP=OM =OQ⇒OP=OQ⇒△OPQ cân tại O
c)△OHP = △OHM⇒∠HOP=∠HOM (2 góc tương ứng)
△OKM = △OKQ⇒∠KOM=∠KOQ (2 góc tương ứng)
Ta có:
∠POQ=∠POH+∠HOM+∠MOK+∠KOQ = 2.(∠HOM+∠MOK)=2.600=1200