Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi \( \angle OAN = \angle OBM = \alpha \) (do chúng cùng nằm giữa OA và OB).
Ta có \( \angle OAB = \angle OBA \) (do OA > OB) và \( \angle OAN + \angle OAB = \angle OBM + \angle OBA = 180^\circ \).
Do đó, theo Định lý cạnh-góc-cạnh, ta có \( \triangle OAN \) đồng dạng với \( \triangle OBM \).
b) Gọi \( \angle AMN = \angle BNM = \beta \) (do chúng cùng nằm giữa AM và BN).
Ta có \( \angle AMB = \angle ANB \) (do \( \triangle OAN \) đồng dạng với \( \triangle OBM \)) và \( \angle AMN + \angle AMB = \angle BNM + \angle ANB = 180^\circ \).
Do đó, theo Định lý cạnh-góc-cạnh, ta có \( \triangle AMN \) đồng dạng với \( \triangle BNM \).

Xét 2 tam giác AOC và tam giác BOC có:
OA = OB (gt)
OC là cạnh chung
góc O1 = góc O2 (vì Om là tia phân giác của góc xOy)
suy ra tam giác AOC = tam giác BOC (c-g-c)
bạn tự vẽ hình và ghi giả thiết kết luận nha
Giải
Xét ΔAOC và ΔBOC, ta có:
OC là cạch chung
O1 = O2 (Vì Om là tia phân giác của góc xOy)
OA = OB (gt)
→ ΔAOC = ΔBOC ( c.g.c)

a: Xét ΔOAM vaf ΔOBM có
OA=OB
góc AOM=góc BOM
OM chung
Do đó; ΔOAM=ΔOBM
b,c: ΔOAM=ΔOBM
nên MA=MB
mà OA=OB
nên OM là đường trung trực của AB
=>OM vuông góc với AB
d: Xét ΔNAB có
NM là đường trung trực của AB
nên ΔNAB cân tại N

a: Xét ΔOMA và ΔOMB có
OM chung
MA=MB
OA=OB
DO đo: ΔOMA=ΔOMB
=>góc AOM=góc BOM
=>OM là phân giác của góc xOy(1)
b: Ta có: ΔOCD cân tại O
mà ON là đường trung tuyến
nên ON là phân giác của góc xOy(2)
Từ (1), (2) suy ra O,M,N thẳng hàng

Tham khảo:
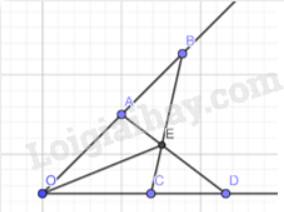
a) Xét \(\Delta OAD\) và \(\Delta OCB\), ta có :
OD = OB
\(\widehat{A}\) chung
OA = OC
\(\Rightarrow \Delta OAD=\Delta OCB\) (c-g-c )
\( \Rightarrow AD = BC\)(2 cạnh tương ứng )
b) Vì \(\Delta OAD=\Delta OCB\) nên \(\widehat{OAD}=\widehat{OCB}; \widehat{D}=\widehat{B}\) ( 2 góc tương ứng)
Mà \(\widehat{OAD}+\widehat{BAD}=180^0\) ( 2 góc kề bù)
\(\widehat{OCB}+\widehat{BCD}=180^0\) ( 2 góc kề bù)
Do đó, \(\widehat{BAD}=\widehat{BCD}\)
Vì \(OA+AB=OB; OC+CD=OD\)
Mà \(OC = OA, OD = OB\)
\(\Rightarrow AB=CD\)
Xét \(\Delta EAB\) và \(\Delta ECD\), ta có:
\(\widehat {ABE} = \widehat {CDE}\)
\(AB = CD\)
\(\widehat {BAE} = \widehat {DCE}\)
\(\Rightarrow \Delta EAB=\Delta ECD\) (g-c-g)
c) Vì \(\Delta EAB=\Delta ECD\) nên EB = ED ( 2 cạnh tương ứng)
Xét \(\Delta OBE\) và \(\Delta ODE\), ta có :
EB = ED
OB = OD
OE chung
\( \Rightarrow \Delta OBE=\Delta ODE \) (c.c.c)
\( \Rightarrow \widehat{BOE}=\widehat{DOE}\) ( 2 góc tương ứng)
\( \Rightarrow \) OE là phân giác \(\widehat {xOy}\)
a) Xét \(\Delta OAN\) và \(\Delta OBM \) có:
OA=OB (gt)
\(\widehat{O}\) chung
OM=ON (gt)
=>\(\Delta OAN = \Delta OBM\)(c.g.c)
b) Do \(\Delta OAN = \Delta OBM\) nên AN=BM ( 2 cạnh tương ứng); \(\widehat {OAN} = \widehat {OBM}\)( 2 góc tương ứng) =>\(\widehat {NAM} = \widehat {MBN}\)
Do OA + AM = OM; OB + BN = ON
Mà OA = OB, OM =ON
=> AM=BN
Xét \(\Delta AMN\) và \(\Delta BNM\) có:
AN=BM (cmt)
\(\widehat {NAM} = \widehat {MBN}\) (cmt)
AM=BN (cmt)
=>\(\Delta AMN = \Delta BNM\)(c.g.c)