
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



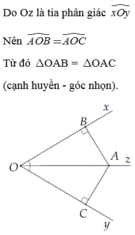
Xét \(\Delta OAB\)và \(\Delta OAC\)có :
\(\widehat{OBA}=\widehat{OCA\left(=90^o\right)}\)
OA là cạnh chung
\(\widehat{O_1}=\widehat{O_2}\left(gt\right)\)
\(\Rightarrow\Delta OAB=\Delta OAC\left(ch-gn\right)\)

a)
Xét \(\Delta\)OAC và \(\Delta\)OBC có:
^CAO = ^CBO ( = 90\(^o\))
OC chung
^AOC = ^BOC ( OC là phân giác ^xOy)
=> \(\Delta\)OAC = \(\Delta\)OBC ( cạnh huyền - góc nhọn) => OA = OB
b) \(\Delta\)OAC = \(\Delta\)OBC => CA = CB ; ^BCO = ^ACO
Xét \(\Delta\)IAC và \(\Delta\)I BC có: CA = CB ; ^BCI = ^ACI ( vì ^BCO = ^ACO ) ; CI chung
=> \(\Delta\)IAC = \(\Delta\)IBC ( c.g.c) (1)
=> IA = IB => I là trung điểm AB (2)
c) từ (1) => ^AIC = ^BIC mà ^AIC + ^BIC = 180\(^o\)
=> ^AIC = ^BIC = \(90^o\)
=> CI vuông góc AB
=> CO vuông goác AB tại I (3)
Từ (2) ; ( 3) => CO là đường trung trực của đoạn thẳng AD.

a: Xet ΔOAP vuông tại A và ΔOBP vuông tại B co
OP chung
góc AOP=góc BOP
=>ΔOAP=ΔOBP
=>OA=OB
=>ΔOAB cân tại O
b: ΔOAB cân tại O
mà OP là phân giác
nên OP vuông góc AB