K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
4 tháng 5 2018
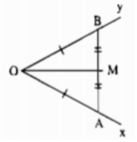
- Dùng thước chia khoảng, trên Ox lấy điểm A, trên Oy lấy điểm B sao cho OA = OB.
- Nối AB.
- Dùng thước chia khoảng để đo đoạn AB, lấy trung điểm M của AB.
- Kẻ tia OM.
Khi đó, OM là tia phân giác của góc ∠xOy.
Chứng minh
Tam giác ABO có OA = OB ( cách dựng) nên tam giác OAB cân tại O.
Lại có: OM là đường trung tuyến nên OM cũng là đường phân giác của ∠(AOB). ( tính chất tam giác cân)
Vậy OM là tia phân giác của ∠(xOy).
16 tháng 3 2023
`a)`
Có `IH⊥Ox=>hat(H_1)=90^0`
`IK⊥Oy=>hat(K_1)=90^0`
Xét `Delta KIO` và `Delta HIO` có :
`{:(hat(K_1)=hat(H_1)(=90^0)),(OI-chung),(IK=IH(GT)):}}`
`=>Delta KIO=Delta HIO(c.h-c.g.v)(đpcm)`
`b)`
Có `Delta KIO=Delta HIO(cmt)=>hat(O_1)=hat(O_2)` ( 2 góc t/ứng )
mà `OI` nằm giữa `Ox` và `Oy(I in hat(xOy))`
nên `OI` là p/g của `hat(xOy)(đpcm)`
KT
0
PD
0
TH
1
bn chép thiếu đề bài ah !!!
mình chép thiếu thật sorry