Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cho tam giác abc có ab = ac tia phân giác góc a cắt bc tại d chứng minh tam giác adb= tam giác adc dh vuông góc với ab dk vuông góc với ac chứng minh dh = dk biết góc bac = 4 nhân với góc abc tính số đo các góc abc

a: Xét ΔOHA vuông tại H và ΔOKB vuông tại K có
OA=OB
ˆOO^ chung
Do đó: ΔOHA=ΔOKB
Suy ra: OH=OK

a, Vì \(\left\{{}\begin{matrix}OA=OB\\AM=MB\\OM.chung\end{matrix}\right.\) nên \(\Delta OAM=\Delta OBM\left(c.c.c\right)\)
b, Vì \(\Delta OAM=\Delta OBM\) nên \(\widehat{AOM}=\widehat{BOM}\)
Do đó OM là p/g góc xOy

Xét 2 tam giác AOC và tam giác BOC có:
OA = OB (gt)
OC là cạnh chung
góc O1 = góc O2 (vì Om là tia phân giác của góc xOy)
suy ra tam giác AOC = tam giác BOC (c-g-c)
bạn tự vẽ hình và ghi giả thiết kết luận nha
Giải
Xét ΔAOC và ΔBOC, ta có:
OC là cạch chung
O1 = O2 (Vì Om là tia phân giác của góc xOy)
OA = OB (gt)
→ ΔAOC = ΔBOC ( c.g.c)

cái đề dài thế này, chả biết khó hay ko nhưng mà ngại làm quá :[
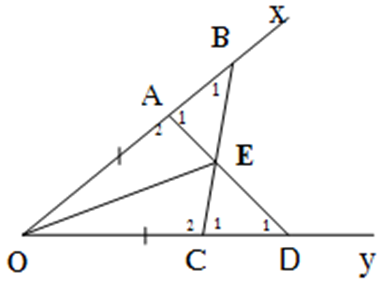
hình như câu b cho đề sai, pải là: ∆EAB=∆ECD mới đúng