Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét \(\Delta OAC\)và \(\Delta OBC\)có:
OA = OB (gt)
\(\widehat{AOC}=\widehat{BOC}\)(Oz là tia p/g của \(\widehat{xOy}\))
OC là cạnh chung
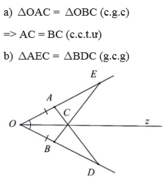
\(\Rightarrow\Delta OAC=\Delta OBC\left(c.g.c\right)\)
\(\Rightarrow AC=BC\)(2 cạnh tương ứng)
b) Ta có: \(\Delta OAC=\Delta OBC\)(theo a)
\(\Rightarrow\widehat{OAC}=\widehat{OBC}\)(2 góc tương ứng)
hay \(\widehat{OAD}=\widehat{OBE}\)
Xét \(\Delta OAD\)và \(\Delta OBE\)có:
\(\widehat{O}\)là góc chung
OA = OB (gt)
\(\widehat{OAD}=\widehat{OBE}\)(cmt)
\(\Rightarrow\Delta OAD=\Delta OBE\left(g.c.g\right)\)
=> AD = BE (2 cạnh tương ứng)
Mà AC = BC (theo a)
=> AD - AC = BE - BC
=> CD = CE
Xét \(\Delta ACE\)và \(\Delta BCD\)có:
AC = BC (cmt)
\(\widehat{ACE}=\widehat{BCD}\)(2 góc đối đỉnh)
CE = CD (cmt)
\(\Rightarrow\Delta ACE=\Delta BCD\left(c.g.c\right)\)

O A D x C I z B E y
Xét tam giác AOC và tam giác BOC
có OC chung
góc BOC= góc AOC (GT)
góc CBO = góc CAO = 900
suy ra tam giác AOC = tam giác BOC ( cạnh huyền- góc nhọn)
suy ra AC=BC ( hai cạnh tương ứng)
b) Xét tam giác BCE và tam giác ACD
có góc EBC = góc DAC = 900
AC=BC ( CMT)
góc BCE = góc ACD ( đối đỉnh)
suy ra am giác BCE =tam giác ACD (g.c.g)
suy ra CE=CD (hai cạnh tương ứng)
suy ra tam giác ECD cân tại C
c)

a: Xét ΔOAC vuông tại A và ΔOBC vuông tại B có
OC chung
góc AOC=góc BOC
=>ΔOAC=ΔOBC
=>OA=OB và CA=CB
b: Xét ΔCAD vuông tại A và ΔCBE vuông tại B có
CA=CB
góc ACD=góc BCE
=>ΔCAD=ΔCBE
=>CD=CE và AD=BE
c: Xét ΔOED có OA/AD=OB/BE
nên AB//ED

a/Xét tam giác OCA và tam giác OCB:
OC chung
OAC=OBC(90 độ)
Góc AOC=BOC(Phân giác Oz)
=> Tam giác OCA=OCB(ch-gn)
=> CA=CB(cạnh tương ứng)
b/ Xét tam giác CAF và tam giác CBE:
Góc ACF=BCE(đối đỉnh)
Góc CBE=CAF(90 độ)
AC=CB(câu a)
=> Tma giác CAF=tam giác CBE(ch-gn)
=> CF=CE(cạnh tương ứng)
=> Tam giác CEF cân tại C
c/Xét tam giác vuông CBE có:
CE là cạnh huyền.
=> CE>CB Mà CB=CA
=> CE>CA(đpcm)
Bạn tự vẽ hình nha![]()
b.
Xét tam giác AFC và tam giác BEC có:
FAC = EBC ( = 90 )
AC = BC (theo câu a)
ACF = BCE (2 góc đối đỉnh)
=> Tam giác AFC = Tam giác BEC (g.c.g)
=> CF = CE (2 cạnh tương ứng)
=> Tam giác CEF cân tại C
c.
Tam giác BCE vuông tại B có:
BC < CE (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà BC = AC (theo câu a)
=> AC < CE
Chúc bạn học tốt![]()

a: Xét ΔOAC vuông tại A và ΔOBC vuông tại B có
OC chung
góc AOC=góc BOC
=>ΔOAC=ΔOBC
b: Xét ΔCAD vuông tại A và ΔCBE vuông tại B có
CA=CB
góc ACD=góc BCE
=>ΔCAD=ΔCBE
=>CE=CD và AD=BE
c: Xét ΔOED có OA/AD=OB/BE
nên AB//ED
Tính diện tích hình thang ABCD , biết diện tích tam BMC là 4,2
bạn bieét làm ko