Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tìm M khi độ OA, OB là bất kì
- Vì M cách đều hai cạnh Ox, Oy của góc xOy nên M nằm trên đường phân giác Oz của góc xOy (1).
- Vì M cách đều hai điểm A, B nên M nằm trên đường trung trực của đoạn AB (2).
Từ (1) và (2) ta xác định được điểm M là giao điểm của đường phân giác Oz của góc xOy và đường trung trực của đoạn AB.
b) Tìm M khi OA = OB
- Vì điểm M cách đều hai cạnh của góc xOy nên M nằm trên đường phân giác của góc xOy (3).
- Ta có OA = OB. Vậy ΔAOB cân tại O.
Trong tam giác cân OAB đường phân giác Oz cũng là đường trung trực của đoạn AB (4).
Từ (3) và (4) ta xác định được vô số điểm M nằm trên đường phân giác Oz của góc xOy thỏa mãn điều kiện bài toán.
a) Vì M cách đều hai cạnh Ox, Oy của ˆxOyxOy^ nên M phải thuộc tia phân giác ˆxOyxOy^.
Vì M cách đều hai điểm A và B nên M thuộc đường trung trực của AB. Vậy M là giao điểm của tia phân giác ˆxOyxOy^ và đường trung trực của đoạn thẳng AB.
b) Nếu OA = OB thì ∆AOB cân tại O nên tia phân giác ˆxOyxOy^ cũng là trung trực của AB nên mọi điểm trên tia phân giác ˆxOyxOy^ sẽ cách đều hai cạnh Ox, Oy và cách đều hai điểm A và B.
Vậy khi OA = OB thì mọi điểm trên tia phân giác ˆxOyxOy^ đều thỏa mãn các điều kiện ở câu a.

Vì điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy).
Vì điểm M cách đều 2 điểm A và B nên M thuộc đường trung trực của AB.
Vậy M là giao điểm của đường trung trực của đoạn thẳng AB và tia phân giác Oz của ∠(xOy)
Do đó, có vô số điểm M thỏa mãn điều kiện trong câu a) khi OA = OB.
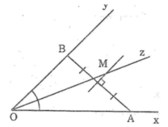

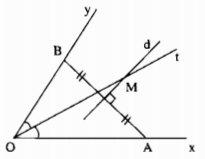
a) - Điểm nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên nó thuộc tia phân giác Ot của góc xOy
- Điểm cách đều 2 điểm A và B thuộc đường thẳng d là đường trung trực của AB
Vậy M là giao điểm của dường trung trực của đoạn thẳng AB và tia phân giác Ot của góc xOy
b) Nếu OA = OB
⇒ ∆OAB cân tại O
Tia phân giác của góc xOy cũng là đường trung trực của AB. Vậy bất kỳ điểm M nào nằm trên tia phân giác của góc xOy đều thỏa mãn điều kiện câu a.

x O y A B C
Ta nối O với A.
Xét \(\Delta OAB\) và \(\Delta OAC\) có :
\(\hept{\begin{cases}\widehat{OBA}=\widehat{OCA=90^o}\\OAchung\\OB=OC\left(gt\right)\end{cases}}\)
\(\Rightarrow\Delta OAB=\Delta OAC\) ( cạnh huyền - cạnh góc vuông )
\(\Rightarrow\widehat{BOA}=\widehat{COA}\)
\(\Rightarrow OA\) là tia phân giác của \(\widehat{xOy}\)
*) Nhận xét : Tập hợp các điểm cách đều hai cạnh của một góc thì nằm trên tia phân giác của góc đó.

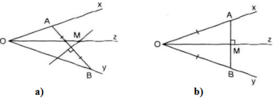
Tìm M khi OA = OB
Nếu OA = OB thì ∆AOB cân tại O nên tia phân giác góc xOy cũng là trung trực của AB.
Do đó mọi điểm trên tia phân giác góc xOy sẽ cách đều hai cạnh Ox, Oy và cách đều hai điểm A và B.
Vậy khi OA = OB thì có vô số điểm M thỏa mãn các điều kiện ở câu a.
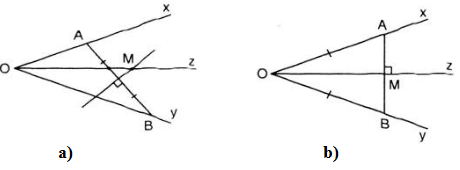

Tìm M khi độ dài đoạn OA, OB là bất kì
- Vì M cách đều hai cạnh Ox, Oy của góc xOy nên M nằm trên đường phân giác Oz của góc xOy (1).
- Vì M cách đều hai điểm A, B nên M nằm trên đường trung trực của đoạn AB (2).
Từ (1) và (2) ta xác định được điểm M là giao điểm của đường phân giác Oz của góc xOy và đường trung trực của đoạn AB.