Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
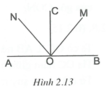a) Ta có
A
O
N
^
+
B
O
N
^
=
180
°
;
B
O
M
^
+
A
O
M
^
=
180
°
(hai góc kề bù) mà
A
O
M
^
=
B
O
N
^
(đề bài cho) nên
A
O
N
^
=
B
O
M
^
.
Mặt khác, tia OC là tia phân giác của góc MON nên C O N ^ = C O M ^ .
Do đó A O N ^ + C O N ^ = B O M ^ + C O M ^ (1)
Ta có tia ON nằm giữa hai tia OA, OC; tia OM nằm giữa hai tia OB, OC nên từ (1) suy ra A O C ^ = B O C ^ = 180 ° : 2 = 90 ° . Vậy O C ⊥ A B .
b) Tia OM nằm giữa hai tia OB và ON nên B O M ^ + M O N ^ = B O N ^ = m ° (1).
Mặt khác B O M ^ = 180 ° − A O M ^ = 180 ° − m ° (2).
Từ (1) và (2) suy ra: 180 ° − m ° + 90 ° = m ° ⇒ 2 m ° = 270 ° ⇒ m ° = 135 ° .
Vậy m = 135 .
Chứng minh một tia là tia phân giác, là tia đối
\(\Rightarrow\widehat{AOM}=\widehat{BON}\)
\(\Rightarrow\widehat{AOM}+\widehat{MOC}+\widehat{CON}+\widehat{NOB}=180^o\)
Mà: \(\widehat{AOM}=\widehat{BON},\widehat{CON}=\widehat{COM}\)
\(\Rightarrow2\widehat{AOM}+2\widehat{MOC}=180^o\)
\(\Rightarrow\widehat{AOM}+\widehat{MOC}=90^o\Leftrightarrow\widehat{AOC}=90^o\)
\(\Rightarrow CO\perp AB\)
Vì góc AOB là góc bẹt => góc AOB = 180 độ
Vì góc AOM = BON mà OC là tia phân giác của góc MON => MOC = NOC =1/2 MON
=> AOM+MOC=BON+NOC
=> AOC = BOC mà AOC+BOC= AOB
=> AOC = BOC = 180 : 2= 90 độ
=> AOC VÀ BOC là góc vuông và OC cắt AB tại O=> OC vuông góc AB
Ta có : Góc COA = góc AOE ; góc BOD = góc BOF
Mà góc BOD + góc COD + góc COA = 180 độ ; góc AOE + góc EOF + góc BOF = 180 độ
=> góc COD = góc EOF = 90 độ
=> OE vuông góc với OF
Hai góc AOC và BOC kề bù nên A O C ^ + B O C ^ = 180 °
⇒ B O C ^ = 180 ° − 150 ° = 30 ° .
Tương tự, ta tính được A O D ^ = 30 ° .
Ta có B O E ^ = A O D ^ = 30 ° (hai góc đối đỉnh).
Suy ra B O C ^ = B O E ^ = 30 ° . (1)
Tia OB nằm giữa hai tia OC và OE. (2)
Từ (1) và (2) ta được tia OB là tia phân giác của góc COE
Đếm góc, đếm tia
Do OC vuông góc với OD
\(\Rightarrow\widehat{COD}=90^o\)
Do OA là tia p.g của \(\widehat{COE}\)
OB là tia p.g của \(\widehat{DOF}\)
\(\Rightarrow\widehat{COD}\)đối đỉnh \(\widehat{EOF}\)
mà \(\widehat{COD}=90^o\)
\(\Rightarrow\widehat{EOF}=90^o\)
mà góc EOF = \(90^o\)
\(\Rightarrow\)OE vuông góc OF
tia Om nằm giữa hai tia OA và OC ; tia ON nằm giữa hai tia OB và OC
do đó : \(\widehat{COA}=\widehat{O_3}+\widehat{O_1}\)và \(\widehat{COB}=\widehat{O_4}+\widehat{O_2}\)
vì \(\widehat{O_1}=\widehat{O_2}\)( gt ) ; \(\widehat{O_3}=\widehat{O_4}\)( vì tia OC là tia phân giác của \(\widehat{MON}\)) nên \(\widehat{COA}=\widehat{COB}\)
\(\widehat{COA}\)và \(\widehat{COB}\)là hai góc kề bù bằng nhau nên \(\widehat{COA}=180^o:2=90^o\)suy ra \(OC⊥AB\)
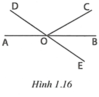
* Tìm cách giải
Để chứng tỏ O M ⊥ A B ta cần chứng tỏ góc AOM (hoặc góc BOM) có số đo bằng 90 ° .
* Trình bày lời giải
Ta có A O E ^ = B O F ^ ; M O E ^ = M O F ^ (đề bài cho)
⇒ A O E ^ + M O E ^ = B O F ^ + M O F ^ (1)
Tia OE nằm giữa hai tia OA, OM; tia OF nằm giữa hai tia OB, OM nên từ (1) suy ra A O M ^ = B O M ^ . Mặt khác, A O M ^ + B O M ^ = 180 ° (hai góc kề bù) nên A O M ^ = 180 ° : 2 = 90 ° , suy ra O M ⊥ O A . Do đó O M ⊥ A B