Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Trên cùng một nửa mặt phẳng bờ chứa tia Oa, ta có: \(\widehat{aOb}< \widehat{aOc}\)
nên tia Ob nằm giữa hai tia Oa và Oc
Suy ra: \(\widehat{aOb}+\widehat{bOc}=\widehat{aOc}\)
hay \(\widehat{bOc}=70^0\)

Có 2 trường hợp
1: Tia Ob và tia Oc cùng thuộc 1 nửa mặt phẳng bờ chứa tia Oa
2: Tia Ob và tia Oc thuộc một nửa mặt phẳng đối nhau bờ chứa tia Oa
Sau đó bạn làm như bình thường sẽ ra đáp án:
Trường hợp 1: a: 5 độ
b: góc dOb = 140 độ, dOc= 145 độ
Trường hợp 2 :a:75 độ
b:góc dOb=140 độ, góc cOd= 145 độ
Chúc bạn làm tốt!!! GOOD LUCK >_<

a) Tia OB nằm giữa hai tia OA và OC
Do đó A O B ^ + B O C ^ = A O C ^
140 + B O C ^ = 160
B O C ^ = 160 - 140 = 20
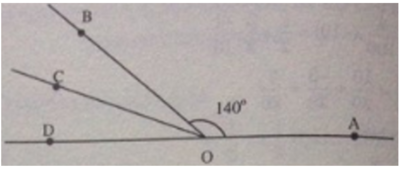
b) Tia OD là tia đối của tia OA, đầu bài cho)
Nên C O D ^ v à A O C ^ kề bù
Ta có C O D ^ + A O C ^ = 180 0
C O D ^ + 160 0 = 180 0
C O D ^ = 180 0 - 160 0 = 20 0
c) Ta có tia OC nằm gữa hai tia OB và OD (1)
Mặt khác C O D ^ = B O C ^ ( =20)(2)
Từ (1) và (2) ta có tia OC là tia phân giác của góc BOD

a/ Vì tia OB là tia phân giác của góc AOC nên tia OB nên ta có :
\(\widehat{AOB}:\frac{1}{2}=\widehat{AOC}\)
\(60^0:\frac{1}{2}=120^0\)
b/ Vì hai góc COD và AOB là hai góc kề bù nên ta có tổng số đo là\(180^0\). Ta có :
\(\widehat{COD}+\widehat{AOC}=\widehat{DOA}\)
\(\widehat{COD}+120^0=180^0\)
\(\widehat{COD}=180^0-120^0\)
\(\widehat{COD}=60^0\)
ĐS:\(\widehat{AOC}=120^0\)
\(\widehat{COD}=60^0\)
Tìm các chữ số a, b sao cho 2018ab đồng thời chia hết cho 5 và 13

a) ta có
BOC=BOA+AOC
40 + 35 = 75
=> BOC= 75
B) ta có
BOD+AOB=AOD
BOD+40 =180 ( vì kề bù )
BOD= 180-40=140
ta có
COD+AOC=AOD
COD+35 = 180 ( vì kề bù )
COD=180-35=145
DAP SO a) 75
b) BOD 140
COD 145