Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(f\left(0\right)=c\in Z\)(1)
\(f\left(1\right)=a+b+c\in Z\)(2)
\(f\left(2\right)=4a+2b+c\in Z\)(3)_
Từ (1), (2) => \(a+b\in Z\)=> \(2a+2b\in Z\)(4)
Từ (1), (3)=> 4a+2b\(\in Z\)(5)
Từ (4), (5) => \(\left(4a+2b\right)-\left(2a+2b\right)\in Z\)
=> \(2a\in Z\)=> \(2b\in Z\)

\(f\left(0\right)=a.0^2+b.0+c=c\) có giá trị nguyên
\(f\left(1\right)=a+b+c\) có giá trị nguyên => a + b có giá trị nguyên
\(f\left(2\right)=4a+2b+c=2a+2\left(a+b\right)+c\)=> 2a có giá trị nguyên
=> 4a có giá trị nguyên
=> 2b có giá trị nguyên.

*f(0) nguyên suy ra 0+0+c=c nguyên
*Vì c nguyên và f(1)=a+b+c nguyên suy ra a+b nguyên
*Tương tự vs f(2)=4a+2b+c suy ra 2a nguyên (Vì 4a+2b và 2(a+b) đều nguyên)
Vì 2a và 2(a+b) nguyên suy ra 2b nguyên (đpcm)

Ko biết là bạn có cần nữa ko.
Nhưng mình vẫn trả lời cho những bạn khác đang cần.
Do P(0) và P(1) lẻ nên ta có:
P(0)=d=> d là số lẻ
P(1)=a+b+c+d => a+b+c+d là số lẻ
Giả sử y là nghiệm nguyên của P(x). Khi đó:
P(y)=ay^3+by^2+cy+d=0
=>ay^3+by^2+cy=-d
Mà d là số lẻ
=>y là số lẻ
Lại có: P(y)-P(1)=(ay^3+by^2+cy+d)-(a+b+c+d)
=a(y^3-1)+b(y^2-1)+c(y-1)+(d-d)
=a(y^3-1)+b(y^2-1)+c(y-1)
Do y là số lẻ=>P(y)-P(1) là số chẵn(1)
Mà P(y)-P(1)= 0-a+b+c+d
=-a-b-c-d
Do a+b+c+d lẻ
=>-a-b-c-d lẻ
Hay P(y)-P(1) là số lẻ(2)
Vì (1) và (2) mâu thuẫn
=> Giả sử sai
Hay f(x) ko thể có nghiệm là các số nguyên(ĐCCM)

1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
11
1
11
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
11
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
11
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
11
1
1
1
1
1
1
1
1
1
1111
1
1111
1
1
1
`
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
111
1
1
1
1
1
1
1
1
1
1
11
1
11
1
1
1
1
1
111
1
1
1
1
1
`
`
1
1
1
1
1
1
1
1
1
1
thay b=-7a vào đa thức f(x)có:
f(x)=ax^2+(-7a)x +c
Ta có:
f(10)=a*10^2-7*a*10+c
=a*100-70a+c
=30a+c (1)
Ta lại có:
f(-3)=a*(-3)^2-7a*(-3)+c
=a*9-(-21)a+c
=30a+c (2)
Từ (1) và (2) suy ra:
f(10),f(-3) ko thể là 1 số âm

Cho f(x)= ax^2 + bx +c thỏa mãn 2a+6b+19c=0
CMR: phương trình ax^2 + bx +c = 0 có nhiệm trong đoạn [0;1/3]
--------
ta có:
f(0) = c
f(1/3) = a/9 + b/3 + c
=> f(0) + 18.f(1/3) = c + 2a + 6b + 18c = 2a + 6b + 19c = 0 (*)
Nếu f(0) = 0 hoặc f(1/3) = 0 => f(x) = 0 có nghiệm là 0 hoặc 1/3 thuộc [0,1/3]
nếu f(0) ≠ 0 và f(1/3) ≠ 0 tự (*) => f(0).f(1/3) ≤ 0 => f(x) = 0 có nghiệm thuộc [0,1/3]
Cho f(x)= ax^2 + bx +c thỏa mãn 2a+3b+6c=0
a) Tính a,b,c theo f(0), f(1), f(1/2)
f(0) = c
f(1) = a + b + c
f(1/2) = a/4 + b/2 + c
b) CMR ba số f(0), f(1), f(1/2) không thể cùng dấu:
f(0) + f(1) + 4f(1/2) = c + a+b+c + a + 2b + 4c = 2a + 3b + 6c = 0
=> f(0) , f(1) , f(1/2) không thể cùng dấu.
Cho f(x)= ax^2 + bx +c thỏa mãn 2a+6b+19c=0
CMR: phương trình ax^2 + bx +c = 0 có nhiệm trong đoạn [0;1/3]
--------
ta có:
f(0) = c
f(1/3) = a/9 + b/3 + c
=> f(0) + 18.f(1/3) = c + 2a + 6b + 18c = 2a + 6b + 19c = 0 (*)
Nếu f(0) = 0 hoặc f(1/3) = 0 => f(x) = 0 có nghiệm là 0 hoặc 1/3 thuộc [0,1/3]
nếu f(0) ≠ 0 và f(1/3) ≠ 0 tự (*) => f(0).f(1/3) ≤ 0 => f(x) = 0 có nghiệm thuộc [0,1/3]
Cho f(x)= ax^2 + bx +c thỏa mãn 2a+3b+6c=0
a) Tính a,b,c theo f(0), f(1), f(1/2)
f(0) = c
f(1) = a + b + c
f(1/2) = a/4 + b/2 + c
b) CMR ba số f(0), f(1), f(1/2) không thể cùng dấu:
f(0) + f(1) + 4f(1/2) = c + a+b+c + a + 2b + 4c = 2a + 3b + 6c = 0
=> f(0) , f(1) , f(1/2) không thể cùng dấu.
:3
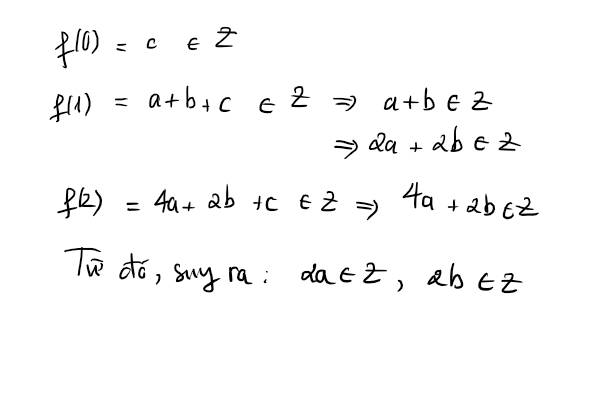
Theo mình hiểu thì $f(x)=ax^2+bx+c$. Thế thì $f(1), f(2)$ hoàn toàn có thể nhận giá trị dương khi $a=-1; c=2; b=2$
Vâng ạ