Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

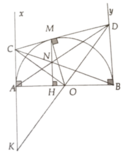
a, Kẻ OM ⊥ CD
Gọi K = OD ∩ d => ∆COK = ∆COD
=> OK = OD => OM = OA = R => CD là tiếp tuyến
b, AC+BD=CM+DM=CD ≥ AB
Do đó min (AC+BD)=AB
<=> CD//AB => ABCD là hình chữ nhật <=> AC = AO
c, AC.BD = MC.MD = O M 2 = 4 a 2
=> 1 O C 2 + 1 O D 2 = 1 4 a 2
d, Từ tính chất hai giao tuyến => MN//BD => MNAB hay MHAB;
AC//BD; MN//BD; NH//BD
=> M N B D = N H B D => MN = NH

a.tứ giác AMDO nội tiếp (∠AOD+∠AMD=180)
⇒BD.BM=BO.BA
mà A,B,O cố định nên BO.BA không đổi
⇒BD.BM không có giá trị phụ thuộc vào vị trí điểm m
b.có ∠EMB=\(\dfrac{1}{2}\stackrel\frown{MB}\) (góc tạo bởi tia tiếp tuyến và dây cung)
do tứ giác AMDO nội tiếp⇒∠MAO=∠MDE(1)
∠MAO=\(\dfrac{1}{2}\stackrel\frown{MB}\)
⇒∠EMB=∠MAO(2)
từ (1) và (2) ⇒∠EMB=∠MDE
⇒ΔEMD cân tại E
⇒ED=EM

a: góc ACO=1/2*sđ cung AO=90 độ
=>OC//BD
Xét ΔADB có
O là trung điểm của AB
OC//BD
=>C là trung điểm của AD
b: BC là tiếp tuyến của (O')
=>góc BCO'=90 độ
=>góc O'CA=góc OCB
=>góc CO'O=góc O'CO=góc O'OC
=>ΔOO'C đều
=>C thuộc (O') sao cho ΔOCO' đều
=>Dựng đường trung trực của OO' cắt (O') tại C, ta đc điểm C cần tìm

a: góc ACO=1/2*sđ cung AO=90 độ
=>OC//BD
Xét ΔADB có
O là trung điểm của AB
OC//BD
=>C là trung điểm của AD
b: BC là tiếp tuyến của (O')
=>góc BCO'=90 độ
=>góc O'CA=góc OCB
=>góc CO'O=góc O'CO=góc O'OC
=>ΔOO'C đều
=>C thuộc (O') sao cho ΔOCO' đều
=>Dựng đường trung trực của OO' cắt (O') tại C, ta đc điểm C cần tìm