Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì M là điểm chính giữa cung AB \(\Rightarrow OM\bot AB\Rightarrow\angle AOM=90=\angle AHM\)
\(\Rightarrow AOHM\) nội tiếp
b) MKBA nội tiếp \(\Rightarrow\angle MKA=\angle MBA=45\) (M là điểm chính giữa)
\(\Rightarrow\Delta MHK\) vuông cân tại H
c) Chu vi của tam giác OPK là: \(OP+OK+PK\)
Ta có: \(\left(OP+OK+PK\right)^2\le3\left(OP^2+OK^2+PK^2\right)\) (BĐT Bunhia)
\(\Rightarrow OP+OK+PK\le\sqrt{3\left(OK^2+OP^2+PK^2\right)}=\sqrt{3.2OK^2}=\sqrt{6}OK\)
Để chu vi tam giác OPK lớn nhất \(\Rightarrow\) OK lớn nhất \(\Rightarrow\) K là điểm chính giữa cung BM

1: góc ACB=1/2*180=90 độ
góc HKB+góc HCB=180 độ
=>CBKH nội tiếp
2: góc MCA=1/2*sđ cung MA
góc ACK=góc MBA=1/2*sđ cung MA
=>góc MCA=góc KCA
=>CA là phân giác của góc MCK

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét tứ giác HCBK có
\(\widehat{HCB}+\widehat{HKB}=180^0\)
Do đó: HCBK là tứ giác nội tiếp
b: Vì HCBK là tứ giác nội tiếp
nên \(\widehat{ACK}=\widehat{HBK}\)
mà \(\widehat{ACM}=\widehat{HBK}\left(=\dfrac{sđ\stackrel\frown{AM}}{2}\right)\)
nên \(\widehat{ACM}=\widehat{ACK}\)

Ta có: góc AKP = 90độ ( Góc nội tiếp chắn nửa đường tròn)
Mà AK giao MN tại H =) Góc HKP = 90độ (1)
Lại có: MC vuông góc AB =) Góc HCB = 90độ (2)
Từ (1) và (2) =) góc HKP + góc HCP = 180độ
Mà 2 góc đối nhau
=) Tứ giác BCHK nội tiếp

1: góc BCA=1/2*180=90 độ
góc HKB+góc HCB=180 độ
=>HCBK nội tiếp
2: góc ACM=1/2*sđ cung AM
góc ACK=góc HCK=góc MBA=1/2*sđ cung AM
=>góc ACM=góc ACK
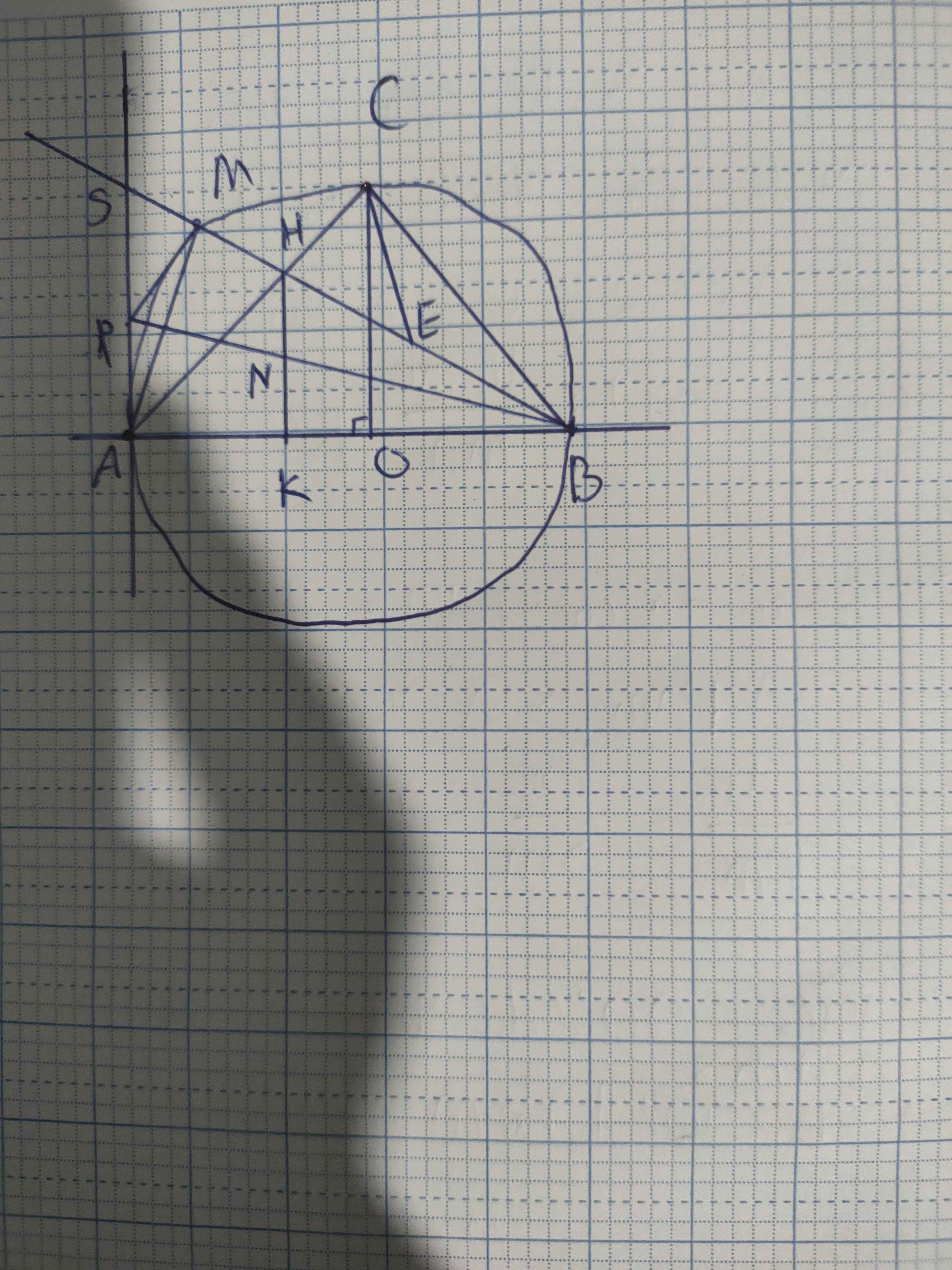



a) ˆAEB=90oAEB^=90o (góc nội tiếp chắn nửa đường tròn) ⇒BE⊥AE⇒BE⊥AE mà CM⊥AECM⊥AE (giả thiết)
⇒BE∥CM⇒ˆCME=ˆMEB⇒BE∥CM⇒CME^=MEB^ (hai góc ở vị trí so le trong)
Mà ˆMCB=ˆMEBMCB^=MEB^ (góc nội tiếp cùng chắn cung MB)
⇒ˆCME=ˆMCB⇒CME^=MCB^ (=ˆMEB)(=MEB^)
⇒⇒ cung CE = cung MB
mà cung MB=cung AM (do M là điểm chính giữa của cung AB)
⇒⇒ cung AM=AM= cung CE⇒AM=CECE⇒AM=CE (1) và
ˆACM=ˆCMEACM^=CME^ (góc nội tiếp cùng chắn 2 cung bằng nhau cung AM=cung CE) mà chúng ở vị trí so le trong nên AC//ME⇒ACEMAC//ME⇒ACEM là hình thang lại có thêm AM=CE (cmt) ⇒ACEM⇒ACEM là hình thang cân
b) Do M là điểm chính giữa của cung AB nên MO⊥ABMO⊥AB
CH⊥ABCH⊥AB (giả thiết)
⇒MO//CH⇒ˆHCM=ˆCMO⇒MO//CH⇒HCM^=CMO^ (hai góc ở vị trí so le trong) (2)
ΔOCMΔOCM cân đỉnh O (OM=OC=R) ⇒ˆMCO=ˆCMO⇒MCO^=CMO^ (3)
Từ (2) và (3) suy ra ˆHCM=ˆMCOHCM^=MCO^
⇒CM⇒CM là phân giác của ˆHCOHCO^ (đpcm)
a) ˆAEB=90oAEB^=90o (góc nội tiếp chắn nửa đường tròn) ⇒BE⊥AE⇒BE⊥AE mà CM⊥AECM⊥AE (giả thiết)
⇒BE∥CM⇒ˆCME=ˆMEB⇒BE∥CM⇒CME^=MEB^ (hai góc ở vị trí so le trong)
Mà ˆMCB=ˆMEBMCB^=MEB^ (góc nội tiếp cùng chắn cung MB)
⇒ˆCME=ˆMCB⇒CME^=MCB^ (=ˆMEB)(=MEB^)
⇒⇒ cung CE = cung MB
mà cung MB=cung AM (do M là điểm chính giữa của cung AB)
⇒⇒ cung AM=AM= cung CE⇒AM=CECE⇒AM=CE (1) và
ˆACM=ˆCMEACM^=CME^ (góc nội tiếp cùng chắn 2 cung bằng nhau cung AM=cung CE) mà chúng ở vị trí so le trong nên AC//ME⇒ACEMAC//ME⇒ACEM là hình thang lại có thêm AM=CE (cmt) ⇒ACEM⇒ACEM là hình thang cân
b) Do M là điểm chính giữa của cung AB nên MO⊥ABMO⊥AB
CH⊥ABCH⊥AB (giả thiết)
⇒MO//CH⇒ˆHCM=ˆCMO⇒MO//CH⇒HCM^=CMO^ (hai góc ở vị trí so le trong) (2)
ΔOCMΔOCM cân đỉnh O (OM=OC=R) ⇒ˆMCO=ˆCMO⇒MCO^=CMO^ (3)
Từ (2) và (3) suy ra ˆHCM=ˆMCOHCM^=MCO^
⇒CM⇒CM là phân giác của ˆHCOHCO^ (đpcm)