Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B O C I P M K Q
a) Đường tròn (O) có đường kính AB và điểm C nằm trên cung AB => ^ACB=900 hay ^PCB=900
Xét tứ giác BCPI: ^PCB=900; ^PIB=900 => Tứ giác BCPI nội tiếp đường tròn (Tâm là trung điểm BP)
b) Xét \(\Delta\)AMB: AC\(\perp\)BM; MI\(\perp\)AB; AC cắt MI tại P => P là trực tâm của \(\Delta\)AMB
Dễ thấy: BK\(\perp\)AM => B;P;K là 3 điểm thẳng hàng (đpcm).
c) Nhận xét: Khi BC=R thì BC=OC=OB=OA => \(\Delta\)ABC là tam giác nửa đều có ^CBA=600
=> ^ACO=300. Do AQ là tiếp tuyến của (O) nên ^ACO+^QCA=900 => ^QCA = 600 (1)
Theo t/c 2 tiếp tuyến cắt nhau => QA=QC (2)
Từ (1) và (2) => \(\Delta\)AQC là tam giác đều => AQ=AC
Dễ có: AC=\(\sqrt{3}R\)=> AQ=\(\sqrt{3}R\)
Xét \(\Delta\)MIB: ^MBI=600; ^MIB=900 => \(\Delta\)MIB là tam giác nửa đều => BI= BM/2
Để ý thấy I là trung điểm OA => BI=3/2R => BM = 2.3/2R = 3R
Dựa vào ĐL Pytagore, ta tính được: \(MI^2=9R^2-\frac{9}{4}R^2=R^2.\left(\frac{36-9}{4}\right)=\frac{R^2.27}{4}\)
\(\Rightarrow MI=\frac{\sqrt{27}.R}{2}\)
\(\Rightarrow S_{QAIM}=\frac{\left(\sqrt{3}R+\frac{\sqrt{27}R}{2}\right).\frac{R}{2}}{2}=\frac{R.\left(\sqrt{3}+\frac{3\sqrt{3}}{2}\right).\frac{R}{2}}{2}\)\(=\frac{R^2.\frac{5\sqrt{3}}{4}}{2}=\frac{5\sqrt{3}.R^2}{8}\)
Vậy \(S_{QAIM}=\frac{5\sqrt{3}.R^2}{8}\).

cho tam giác ABC ( AB<AC) có ba góc nhọc nội tiếp đường tròn tâm (O) và D là hình chiếu của B trên AO sao cho D nằm giữa A và O. gọi M là trung điểm của BC, N là giao điểm của BD và AC, F là giao điểm của MD và AC, E là giao điểm thứ hai của BD với (O), H là giao điểm của BF và AD.
1/ chứng minh tứ giác BDOM nội tiếp và góc MOD + NAE=180.
2/ chứng minh DF //CE.
3/ chứng minh CA là tia phân giác của góc BCE
4/ Chứng minh HN vuông góc với AB

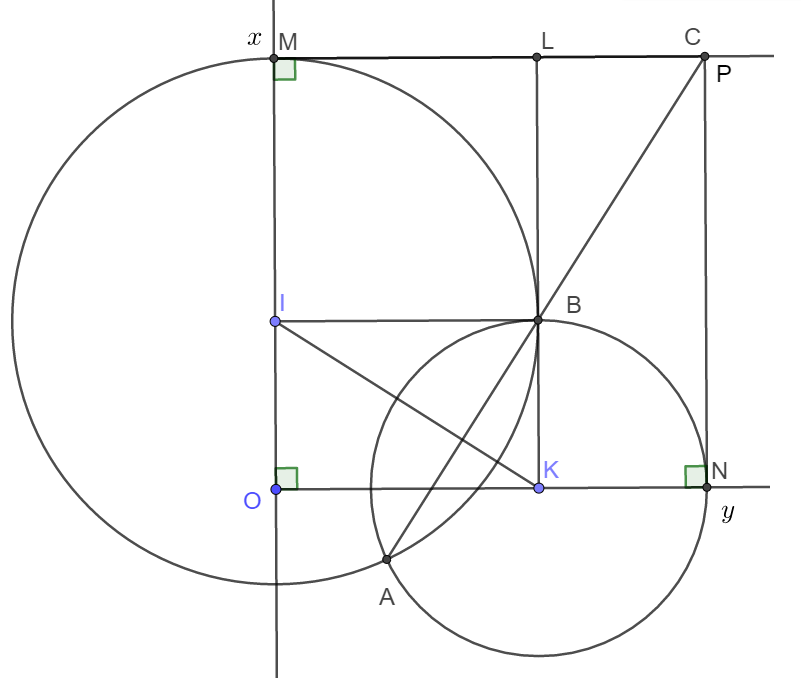
a) Trong tam giác OIK có:
|OK −− OI| < IK < |OK + OI| hay ∣R−r∣<IK<∣R+r∣∣R−r∣<IK<∣R+r∣.
Vậy hai đường tròn (I) và (K) luôn cắt nhau.
b) Dễ thấy tứ giác OMCN là hình chữ nhật (Tứ giác có 3 góc vuông).
Mà OM = OI + IM = OI + OK;
ON = OK + KN = OK + OI.
Vậy OM = ON hay hình chữ nhật OMCN là hình vuông.
c) Gọi giao điểm của BK và MC là L và giao điểm của AB với MC là P.
Tứ giác IBKO là hình chữ nhật. Suy ra IB = OK.
Tứ giác MLBI là hình vuông nên ML = BI, BL = OK.
Từ đó suy ra ΔBLP=ΔKOIΔBLP=ΔKOI. Vì vậy LP = OI.
Suy ra MP = ON = MC. Hay điểm C trùng với P.
Suy ra ba điểm A, B, C thẳng hàng.
d) Nếu OI + OK = a (không đổi) thì OM = MC = a không đổi. Suy ra điểm C cố định.
Vậy đường thẳng AB luôn đi qua điểm C cố định.
