Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M A C x B D y H K O I
a) Tam giác AMC vuông tại M có MH là đường cao
\(\Rightarrow MH=\sqrt{AH.BH}\)( hệ thức lượng trong tam giác vuông )
\(\Rightarrow MH=\sqrt{15}\left(cm\right)\)
b) Vì AC song song với BD nên ta có : \(\frac{AC}{BD}=\frac{AI}{ID}=\frac{CM}{MD}\)( vì \(AC=CM;BD=MD\))
\(\Rightarrow MI//AC\)mà \(MH//AC\) ( cùng vuông góc với AB )
Suy ra \(M,I,H\)thẳng hàng
c ) Đặt \(AB=a,AM=c,BM=b\)
Ta có:
\(AK=\frac{a+c-b}{2};BK=\frac{a+b-c}{2}\)
\(\Rightarrow AK.BK=\frac{a+c-b}{2}.\frac{a+b-c}{2}=\frac{1}{2}.\left[\frac{\left(a+c-b\right)\left(a+b-c\right)}{2}\right]\)
\(=\frac{1}{2}\left[\frac{a^2-\left(b-c\right)^2}{2}\right]=\frac{1}{2}\left[\frac{a^2-\left(b^2+c^2\right)+2bc}{2}\right]\)
\(=\frac{1}{2}.\frac{2bc}{2}=\frac{1}{2}.bc=\frac{1}{2}AM.MB=S_{AMB}\)
Vậy \(S_{AMB}=AK.KB\)
Chúc bạn học tốt !!!

A B E F x y M K O
a)\(\hept{\begin{cases}Ax⊥AB\\By⊥AB\end{cases}}\)=> Ax // By.\(\Delta KFB\)có EA // FB nên\(\frac{KF}{KA}=\frac{BF}{AE}\)(hệ quả định lí Ta-lét) mà EA = EM ; FM = FB (tính chất của 2 tiếp tuyến)
\(\Rightarrow\Delta AEF\)có\(\frac{KF}{KA}=\frac{MF}{ME}\)nên MK // AE (định lí Ta-lét đảo) mà\(AE⊥AB\Rightarrow MK⊥AB\)
b)\(\widehat{EOM}=\frac{\widehat{AOM}}{2};\widehat{FOM}=\frac{\widehat{MOB}}{2}\)(tính chất 2 tiếp tuyến) mà\(\widehat{EOM}+\widehat{FOM}=180^0\)(kề bù)
\(\Rightarrow\widehat{EOF}=\widehat{EOM}+\widehat{FOM}=\frac{180^0}{2}=90^0\)
\(\Rightarrow\Delta EOF\)vuông tại O có OE + OF > EF (bđt tam giác) ; OE + OF < 2EF (vì OE,OF < EF)
\(\Rightarrow1< \frac{OE+OF}{EF}< 2\Rightarrow2< \frac{P_{EOF}}{EF}< 3\Rightarrow\frac{1}{3}< \frac{EF}{P_{EOF}}< \frac{1}{2}\)(1)
Hình thang AEFB (AE // FB) có diện tích là :\(\frac{\left(AE+FB\right).AB}{2}=\frac{\left(EM+FM\right).2R}{2}=EF.R\)
SAEO = SMEO vì có đáy OA = OM ; đường cao AE = ME\(\Rightarrow S_{MEO}=\frac{1}{2}S_{AEMO}\)
SFOM = SFOB vì có đáy FM = FB ; đường cao OM = OB\(\Rightarrow S_{FOM}=\frac{1}{2}S_{MFBO}\)
\(\Rightarrow S_{EOF}=\frac{1}{2}\left(S_{AEMO}+S_{MFBO}\right)=\frac{EF.R}{2}\).Từ tâm đường tròn nội tiếp I của\(\Delta EOF\)kẻ các đường vuông góc với OE,OF,EF thì\(S_{EOF}=S_{EIF}+S_{EIO}+S_{OIF}\)\(\Leftrightarrow\frac{EF.R}{2}=\frac{EF.r+EO.r+OF.r}{2}\)
\(\Rightarrow EF.R=P_{EOF}.r\Rightarrow\frac{r}{R}=\frac{EF}{P_{EOF}}\)(2).Thay (2) vào (1) ta có đpcm.

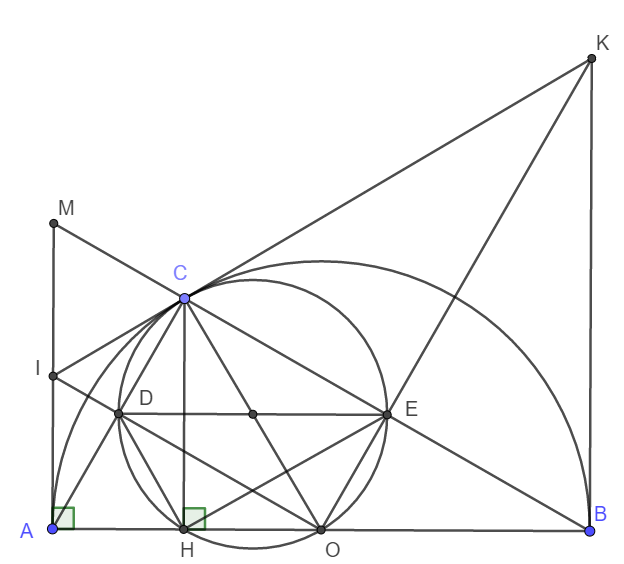
a) Do C thuộc nửa đường tròn nên \(\widehat{ACB}=90^o\) hay AC vuông góc MB.
Xét tam giác vuông AMB có đường cao AC nên áp dụng hệ thức lượng ta có:
\(BC.BM=AB^2=4R^2\)
b) Xét tam giác MAC vuông tại C có CI là trung tuyến ứng với cạnh huyền nên IM = IC = IA
Vậy thì \(\Delta ICO=\Delta IAO\left(c-c-c\right)\)
\(\Rightarrow\widehat{ICO}=\widehat{IAO}=90^o\)
Hay IC là tiếp tuyến tại C của nửa đường tròn.
c) Xét tam giác vuông AMB có đường cao AC, áp dụng hệ thức lượng ta có:
\(MB.MC=MA^2=4IC^2\Rightarrow IC^2=\frac{1}{4}MB.MC\)
Xét tam giác AMB có I là trung điểm AM, O là trung điểm AB nên IO là đường trung bình tam giác ABM.
Vậy thì \(MB=2OI\Rightarrow MB^2=4OI^2\) (1)
Xét tam giác vuông MAB, theo Pi-ta-go ta có:
\(MB^2=MA^2+AB^2=MA^2+4R^2\) (2)
Từ (1) và (2) suy ra \(4OI^2=MA^2+4R^2.\)
d) Do IA, IC là các tiếp tuyến cắt nhau nên ta có ngay \(AC\perp IO\Rightarrow\widehat{CDO}=90^o\)
Tương tự \(\widehat{CEO}=90^o\)
Xét tứ giác CDOE có \(\widehat{CEO}=\widehat{CDO}=90^o\)mà đỉnh E và D đối nhau nên tứ giác CDOE nội tiếp đường tròn đường kính CO.
Xét tứ giác CDHO có: \(\widehat{CHO}=\widehat{CDO}=90^o\) mà đỉnh H và D kề nhau nên CDHO nội tiếp đường tròn đường kính CO.
Vậy nên C, D, H , O, E cùng thuộc đường tròn đường kính CO.
Nói cách khác, O luôn thuộc đường tròn ngoại tiếp tam giác HDE.
Vậy đường tròn ngoại tiếp tam giác HDE luôn đi qua điểm O cố định.
TK:
a.
xét tứ giác BDMI ta có : IMD = 90 (CD ⊥ MI)
IBD = 90 (BD là tiếp tuyến)
mà 2 góc này ở vị trí đối nhau ⇒tứ giác BDMI là tứ giác nội tiếp
⇒ DMB = DIB (2 góc nội tiếp cùng chắng cung DB của tứ giác BDMI) (1)
xét tứ giác ACMI ta có : IAC = 90 (AC là tiếp tuyến)
IMC = 90 (CD ⊥ MI)
mà 2 góc này ở vị trí đối nhau ⇒⇒ tứ giác ACMI là tứ giác nội tiếp
⇒ CMA = CIA (2 góc nội tiếp cung chắng cung AC của tứ giác ACMI) (2)
mà CMA + DMB = 90 (góc AMB là góc nội tiếp chắng nửa (o)) (3)
tứ (1) ; (2) và (3) ta có : CIA + DIB = 90
⇒ CID = 180 - 90 = 90
xét tứ giác MIEF ta có : AMB = 90 (góc nội tiếp chắng nửa (o))
CID = 90 (chứng minh trên)
mà 2 góc này ở vị trí đối nhau ⇒ tứ giác MIEF là tứ giác nội tiếp (đpcm)
TK:b) ta có
\(\widehat{MEF}\)=\(\widehat{MIE}\)=\(\widehat{MIC}\)=\(\widehat{MAC}\)=\(\widehat{MBA}\)
⇒ EF // AB (đpcm)
c.
Ta có \(\widehat{AMO}\)=\(\widehat{OAM}\)=\(\widehat{IAM}\)=\(\widehat{ICM}\)=\(\widehat{MCE}\)
→OM là tiếp tuyến của (CME và DFM)