Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
, suy ra AOMB là tứ giác nội tiếp.
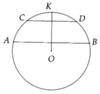
Ta lấy K là điểm chính giữa cung nhỏ A B ⏜
Ta chứng minh được C K ⏜ = K D ⏜
Từ đó ta có OK ⊥ CD, OK ⊥ AB => CD//AB
a: Xét ΔAPE và ΔACP có
góc APE=góc ACP
góc PAE chung
=>ΔAPE đồng dạng với ΔACP
=>AP^2=AE*AC=AN^2
Xét ΔAND và ΔABN có
góc AND=góc ABN
góc NAD chung
=>ΔAND đồng dạng với ΔABN
=>AD*AB=AN^2
=>AD*AB=AE*AC
=>AD/AC=AE/ABB
=>ΔADE đồng dạng vơi ΔACB
=>góc ADE=góc ACB
b: góc ADE=góc ACB
=>góc BDE+góc BCE=180 độ
=>BDEC nội tiếp
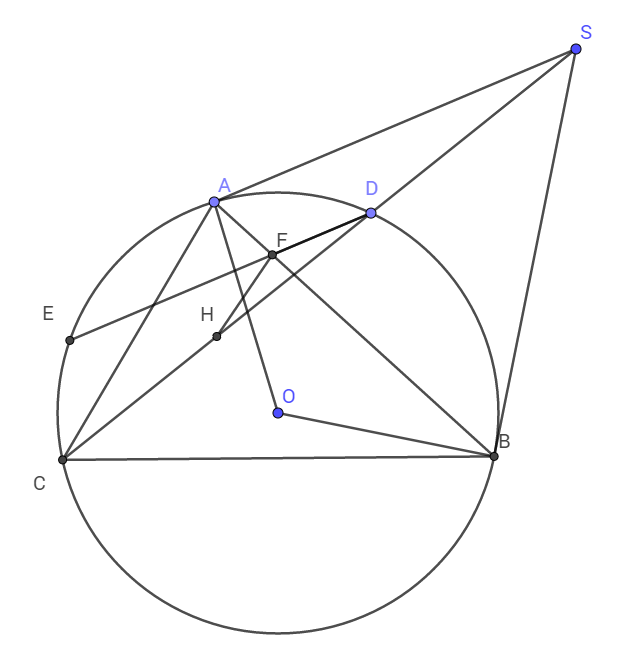
Ta có các tam giác vuông AOS; HOS, BOS có chung cạnh huyền OS nên S, A, H, O, B nội tiếp đường tròn đường kính OS.
Khi đó ta có :
\(\widehat{ASH}=\widehat{ABH}\) (Hai góc nội tiếp cùng chắn cung AH)
Mà \(\widehat{ASH}=\widehat{FDH}\) (Hai góc đồng vị)
\(\Rightarrow\widehat{ABH}=\widehat{FDH}\)
Suy ra tứ giác HFDO nội tiếp.
Từ đó ta có \(\widehat{FHD}=\widehat{ABD}\)(Hai góc nội tiếp)
Mà \(\widehat{ABD}=\widehat{ACD}\) (Hai góc nội tiếp)
Nên \(\widehat{FHD}=\widehat{ACD}\)
Chúng lại ở vị trí đồng vị nên HF // AC.
a, Xét tứ giác AKCH có: \(\widehat{AKC}+\widehat{AHC}=90+90=180\)=> tứ gác AKCH nội tiếp
b,Tứ giác AKCH nội tiếp => \(\widehat{HCK}=\widehat{HAD}\)(góc trong và góc ngoài đỉnh đối diện)
Mặt khác: \(\widehat{HAD}=\widehat{BCD}=\frac{1}{2}sđ\widebat{BD}\)
=> \(\widehat{BCD}=\widehat{ACD}\)=> CD là phân giác \(\widehat{KCB}\)
c, Tứ giác AKCH nội tiếp: => \(\widehat{CKE}=\widehat{CAH}\)
Mà: \(\widehat{CDB}=\widehat{CAH}=\frac{1}{2}sđ\widebat{BC}\)
=> \(\widehat{CKE}=\widehat{CDE}\)=> tứ giác CKDE nội tiếp
=> \(\widehat{CKD}+\widehat{CED}=180\Rightarrow\widehat{CED}=180-\widehat{CKD}=180-90=90\)
=> \(CE⊥BD\)(ĐPCM)
d, em xem lại xem có gõ sai đề không nhé
Câu d) Khi C di chuyển trên cung nhỏ̉ AB. Xác định vị trí C để CK.AD+CE.DB có giá trị lớn nhất.
Nhờ mọi người giải dùm e với.
a.xét tứ giác AOMB có
∠AOB = ∠ AMB (góc ở tâm cùng chắn cung AB)
=> Tứ giác AOMB nội tiếp
b.vì AD//BC ⇒ ABCD là hình thang, hình thang ABCD lại nội tiếp O
⇒ ABCD là hình thang cân
mà M là giao điểm hai đường chéo
⇒ MB = MC (tính chất hình thang cân)
ΔOMB và ΔOMC có:
OB = OC = R
OM chung
MB = MC (cmt)
⇒Δ OMB =Δ OMC (c.c.c)
⇒góc MOB = góc MOC (góc tương ứng)
⇒OM là đường phân giác góc BOC hay đường phân giác góc BOC của ΔOBC
Mà ΔOBC là tam giác cân tại O (có OB = OC = R)
⇒OM là đường trung trực của tam giác cân OBC
⇒OM ⊥BC (đpcm)
c.vì OM ⊥ BC⇒OM thẳng góc AD
⇒theo tính chất dây và đường kính OM là trung trực của AD và BC
có d//AD
⇒d thẳng góc OM
vì AB cố định nên đường thẳng OM không đổi
vì đường thẳng OM không đổi mà d luôn thẳng góc OM
⇒ d đi qua một điểm cố định trên cung AB nhỏ (đpcm)
Dễ thấy b = 1, d = 2, e = 4 đặt y = x2 – 2 suy ra y2 = x4 – 4x2 + 4
Biến đổi P(x) = x4 – 4x2 + 4 – x3 – 6x2 + 2x
= (x2 – 2)2 – x(x2 – 2) – 6x2
Từ đó Q(y) = y2 – xy – 6x2
Tìm m, n sao cho m.n = - 6x2 và m + n = - x chọn m = 2x, n = -3x
Ta có: Q(y) = y2 + 2xy – 3xy – 6x2
= y(y + 2x) – 3x(y + 2x)
= (y + 2x)(y – 3x)
Do đó: P(x) = (x2 + 2x – 2)(x2 – 3x – 2).
* Nếu đa thức P(x) có chứa ax4 thì có thể xét đa thức Q(x) = P(x)/a theo cách trên.