Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác vuông ABO có đường cao BK, áp dụng hệ thức lượng trong tam giác ta có:
\(OB^2=OK.OA\Rightarrow5^2=OK.10\Rightarrow OK=2,5\left(cm\right)\)
b) Xét tam giác cân OBC có OK là đường cao nên đồng thời là phân giác.
Vậy thì \(\widehat{BOA}=\widehat{COA}\)
Suy ra \(\Delta ABO=\Delta ACO\left(c-g-c\right)\Rightarrow\widehat{ACO}=\widehat{ABO}=90^o\)
Vậy nên AC là tiếp tuyến của đường tròn (O).
c) Ta thấy ngay \(\Delta KOI\sim\Delta HOA\left(g-g\right)\Rightarrow\frac{OI}{OA}=\frac{OK}{OH}\Rightarrow OI=\frac{OK.OA}{OH}\)
Xét tam giac vuông ABO có BK là đường cao nên áp dụng hệ thức lượng trong tam giác ta có:
\(OK.OA=OB^2=R^2\) không đổi. Lại có OH cũng không đổi (bằng khoảng cách từ O tới đường thẳng xy)
Vậy nên \(OI=\frac{R^2}{OH}\) không đổi.
Vậy khi A di chuyển trên đường thẳng xy thì độ dài đoạn thẳng OI không đổi.

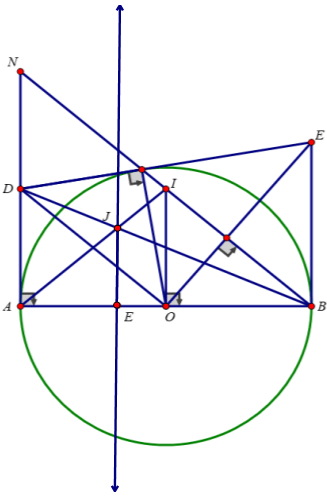
a: Xét tứ giác ODAE có
góc ODA+góc OEA=180 độ
=>ODAE là tứ giác nội tiếp
b: \(AE=\sqrt{\left(3R\right)^2-R^2}=2\sqrt{2}\cdot R\)
\(OI=\dfrac{OE^2}{OA}=\dfrac{R^2}{3R}=\dfrac{R}{3}\)
c: Xét ΔDIK vuông tại I và ΔDHE vuông tại H có
góc IDK chung
=>ΔDIK đồng dạng vơi ΔDHE
=>DI/DH=DK/DE
=>DH*DK=DI*DE=2*IE^2

\(\text{a) Xét tứ giác ADMO có:}\)
∠DMO =90o (do M là tiếp tuyến của (O))
∠DAO =90o (do AD là tiếp tuyến của (O))
=> ∠DMO + ∠DAO = 180o
=> Tứ giác ADMO là tứ giác nội tiếp.
\(\text{b) Do D là giao điểm của 2 tiếp tuyến DM và DA nên OD là tia phân giác của ∠AOM}\)
=>(AOD = \(\frac{1}{2}\)∠AOM
Mặt khác ta có (ABM là góc nội tiếp chắn cung AM
=> ∠ABM = \(\frac{1}{2}\)∠AOM
=> ∠AOD = ∠ABM
Mà 2 góc này ở vị trí đồng vị
=> OD // BM
Xét tam giác ABN có:
OM// BM; O là trung điểm của AB
=> D là trung điểm của AN
c) Ta có: ΔOBM cân tại O ;OE ⊥MB =>OE là đường trung trực của MB
=>EM = EB => ΔMEB cân tại E => ∠EMB = ∠MEB (1)
ΔOBM cân tại O => ∠OMB = ∠OBM (2)
Cộng (1) và (2) vế với vế, ta được:
∠EMB + ∠OMB = ∠MEB + ∠OBM ⇔ ∠EMO =∠EOB ⇔ ∠EOB =90o
=>OB ⊥ BE
Vậy BE là tiếp tuyến của (O).
d) Lấy điểm E trên tia OA sao cho OE = \(\frac{OA}{3}\)
Xét tam giác OAI có OI vừa là đường cao vừa là trung tuyến
=> Tam giác OAI cân tại I => IA = IB; ∠IBA = ∠IAB
Ta có:
\(\hept{\begin{cases}\widehat{IBA}=\widehat{IAB}\\\widehat{IBA}+\widehat{INA}=90^0\\\widehat{NAI}+\widehat{IAB}=\widehat{NAB}=90^0\end{cases}}\)
=> ∠NAI = ∠INA => ΔINA cân tại I => IA = IN
Tam giác NAB vuông tại A có: IA = IN = IB
=> IA là trung tuyến của tam giác NAB
Xét ΔBNA có:
IA và BD là trung tuyến; IA ∩ BD = {J}
=> J là trọng tâm của tam giác BNA
Xét tam giác AIO có:
\(\frac{\text{AJ}}{AI}=\frac{AE}{A0}=\frac{2}{3}\Rightarrow\text{JE}\text{//}OI\)
=> J nằm trên đường thẳng d vuông góc với AB và cách O một khoảng bằng R/3.
Phần đảo: Lấy điểm J' bất kì thuộc đường thẳng d
Do d// OI (cùng vuông góc AB) nên ta có:
\(\frac{\text{AJ}}{AI}=\frac{AE}{A0}\)
\(\text{MÀ}\frac{AE}{AO}=\frac{2}{3}\Rightarrow\frac{\text{AJ}}{AI}=\frac{2}{3}\)
AI là trung tuyến của tam giác NAB
=> J' là trọng tâm tam giác NAB
Vậy khi M di chuyển trên (O) thì J di chuyển trên đường thẳng d vuông góc với AB và cách O một khoảng là R/3.
HÌNH Ở TRONG THỐNG KÊ HỎI ĐÁP NHA