Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
OM là bán kính
EF\(\perp\)OM tại M
Do đó: EF là tiếp tuyến của (O)
b: Xét (O) có
EM,EA là các tiếp tuyến
Do đó: EM=EA
Xét (O) có
FM,FB là các tiếp tuyến
Do đó: FM=FB
Ta có: EF=EM+MF
mà EM=EA và FM=FB
nên EF=EA+FB

bài làm
a, gọi H là tiếp điểm của tiếp tuyến MN
theo giả thuyết 2 tiếp tuyến AM và MH cắt nhau tại M
⇒ AM=MH ( tính chất 2 tiếp tuyến cắt nhau)
theo giả thuyết 2 tiếp tuyến HN cắt BN tại N
⇒ HN=BN ( tính chất 2 tiếp tuyến cắt nhau)
nên ta có: MN=HM=HN=\(\dfrac{1}{2}\)(AOH =HON)=90 độ
vậy góc MON=90 đọ và là tâm giác vuông tại O đường cao OH
b,theo giả thuyết 2 tiếp tuyến AM và MH cắt nhau tại M
⇒ AM=MH ( tính chất 2 tiếp tuyến cắt nhau)
theo giả thuyết 2 tiếp tuyến HN cắt BN tại N
⇒ HN=BN ( tính chất 2 tiếp tuyến cắt nhau)
Theo hệ thức lượng trong tam giác vuông: OI^2=MI.INOH2=MH.HNAM.BN=MI.NI=OI^
Vì vậy AM.BN=MI.NI=OI^2=R^2AM.BN=MH.NH=
\(OH^2\)=\(R^2\)

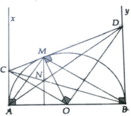
a, Từ CA, CM là tiếp tuyến của (O) chứng minh được A,C,M,O ∈ đường tròn bán kính O C 2
b, Chứng minh OC,BM cùng vuông góc với AM . từ đó suy ra OC//BM
c, S A C D B = A C + B D A B 2 = A D . A B 2
=> S A C D B nhỏ nhất khi CD có độ dài nhỏ nhất
Hay M nằm chính giữa cung AB
d, Từ tính chất hai giao tuyến => AC = CM và BM=MD, kết hợp với AC//BD
ta chứng minh được C N N B = C M M D => MN//BD => MN ⊥ AB

a: Xét (O) có
AE là tiếp tuyến
AM là tiếp tuyến
Do đó: AE=AM
Xét (O) có
FM là tiếp tuyến
FB là tiếp tuyến
Do đó: FM=FB
Ta có: FM+EM=EF
nên FE=AE+BF