Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ngủ đi , bây giờ chẳng bạn nào giải đâu !!!
Chúc học giỏi !!!

M A B O C
a, có AM = 2AC mà để AM lớn nhất
<=> AC lớn nhất
có AC là dây cung của đường tròn (O) đk AB
=> AC =< AB
dấu = xảy ra khi C trùng B
b, AM = 2R.căn 3 mà AM = 2AC
<=> 2AC = 2R.căn 3
<=> AC = R.căn 3
xét tam giác ABC vuông tại C => AC^2 + CB^2 = AB^2
Mà BA = 2R
=> (R.căn 3)^2 + BC^2 = (2R)^2
<=> 3R^2 + BC^2 = 4R^2
<=> BC^2 = R^2
<=> BC = R
vậy lấy điểm C trên (O) sao cho BC = R để AM = 2R.căn 3
c, xét tam giác BAM có BC là đường trung tuyến đồng thời là đường cao
=> tam giác BAM cân tại B
=> BA = BM mà AB không đổi
=> BM không đổi
=> khi C di động trên (O) thì M di động trên đường tròn (B) cố định

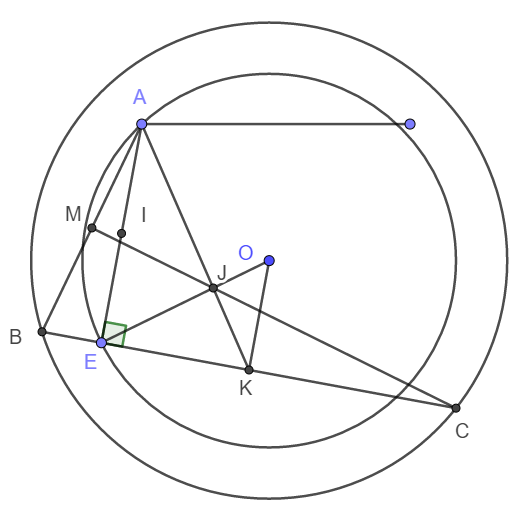
a) Gọi I, K lần lượt là trung điểm của AE và BC.
Ta có : \(EB^2=\left(BK-EK\right)^2;EC^2=\left(KC+EK\right)^2\)
\(\Rightarrow EB^2+EC^2=2\left(BK^2+EK^2\right)=2\left(BO^2-OK^2+OE^2-OK^2\right)\)
\(=2\left(R^2+r^2\right)-4OK^2\)
\(AE^2=4AI^2=4\left(r^2-OI^2\right)\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+6r^2-4\left(OI^2+OK^2\right)\)
Mà OIEK là hình chữ nhật nên \(OI^2+OK^2=OE^2=r^2\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+2r^2\) không đổi.
b) Giả sử EO giao với AK tại J.
Vì IOEK là hình chữ nhật nên OK song song và bằng EI. Vậy nên OK song song và bằng một nửa AE.
Do đó \(\frac{JE}{JO}=\frac{AJ}{JK}=\frac{AE}{OK}=2\)
Vì OE cố định nên J cố định; Vì AK là trung tuyến của tam giác ABC nên J là trọng tâm tam giác ABC
Suy ra J thuộc MC.
Vậy MC đi qua J cố định.
c) Vì AK = 3/2AJ nên H trùng K.
Do đó OH vuông góc BC. Suy ra H thuộc đường tròn đường kính OE.

Phần thuận: giả sử M là trung điểm của dây AB. Ta có OM ⊥ AB (định lí)
Khi B di động trên (O), điểm M luôn nhình OA cố định dưới góc vuông , vậy M thuộc đường tròn đường kính OA.
Phần đảo: lấy điểm M' bất kì trên đường tròn đường kính OA.
Nối M' với A, đường thẳng M'A cắt đường tròn (O) tại B'. Nối M' với O ta có

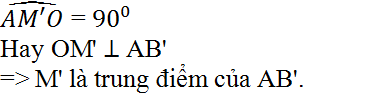
theo định lý Pytago ta có :
\(OM=\sqrt{OA^2-AM^2}=\sqrt{R^2-\left(\frac{AB}{2}\right)^2}=\frac{R}{2}=const\)\
Vậy khi AB di chuyển thì M thuộc đường tròn tâm O bán kính R/2