Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ac là tiếp tuyến (o;r) =) ao vuông góc ac (1
db là tiếp tuyến (o; r)=) ob vuông góc db (2
từ 1, và 2 =) ac//db
=) tứ giac cabd là hình thang
b, dm là tiếp tuyến (o;r)
db là tiếp tuyến (o;r)
=) góc mod bằng góc bod (3)
xét tam giác mon và tam giác bon có :
góc mod = góc bod ( cmt )
mo=ob=r
on chung
=) tam giác mon và tam giác bon bằng nhau ( cgc)
=) mn=nb
lại có :
ao=ob ( =r)
mn=nb (cmt)
=) no là đường trung bình tam giác mab =) no//ma
mà ma vuông mb ( do mo=oa=ob =r => tam giác mab vuông tại m )
=) mb vuông no
hay do vuông mb
tá có : tam giác aeb vuông tại e ( eo=bo=ao=r )
xét tam giác dab
de*da = db^2
xét tam giác : dbo
dn*do=db^2
=) dn*do=de*da
c,
ma//no (cmt )
=> góc dob =góc mao
xét tam giác fao và tam giác dob
góc dob = góc mao
ao=ob (=r)
góc foa = góc dbo
=> tam giác foa = tam giác dbo ( cgv-gn)
fo= db
lại ó : fo vuông ab
db uông ab
=> fo//db (4 )
fo=bd (cmt ) (5)
từ 4, 5 => tứ giác fobd là hình thang
tứ giác fobd là hình thang mà fo vuông ab => tứ giác fobd là hình chữ nhật
d, kẻ cl vuông góc ma vì cm=ca ( mc là tiếp tuyến (o;r) , ca là tiếp tuyến (o;r) )=> tam giác cma là tam giác cân
mà cl lại vuông ma => ml=la hay la= ma/2=r/2
lại có tam giác mao là tam giác đều ( ma=ao=mo=r) => góc mao= 60 độ
góc cam = góc cao - góc mao = 90-60=30 độ
xét tam giác cla vuông tại l
ca= la / cos góc A
ac = (r/2 )/ ( (căn 3)/2 ) = r/(căn 3)
ab = r*2
vì no là đường phân giác tam giác mab => no= 1/2 ma = r/2
xét tam giác dob có :
no*do=ob^2
(r/2)*do=r^2
=> do= r2
xét tam giác dob vuông tại b theo định lý pitago :
do^2- ob^2= db^2 = (r2)^2 - ( r^2)= r^2*3=> db = căn ( r^2*3) = r căn 3
diện tích hình thang :
((ac+db )*ab)/2 = (r^2*4)/căn 3
c

a: Xét tứ giác ACDB có
AC//BD
góc BAC=90 độ
Do đó: ACDB là hình thang vuông
b: Xét (O) có
DM,DB là các tiếp tuyến
nên DM=DB
mà OM=OB
nên OD là đường trung trực của MB
=>DO vuông góc với MB
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đo: ΔAMB vuông tại M
=>AM//OD
c: Xét (O) có
CM,CA là các tiếp tuyến
nên CM=CA
mà OA=OM
nên OC là đường trung trực của AM
OE*OC=OM^2
OF*OD=OM^2
Do đó: OE*OC=OF*OD

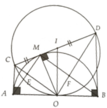
a, Dễ thấy A M B ^ = 90 0 hay E M F ^ = 90 0 tiếp tuyến CM,CA
=> OC ⊥ AM => O E M ^ = 90 0 Tương tự => O F M ^ = 90 0
Chứng minh được ∆CAO = ∆CMO => A O C ^ = M O C ^
=> OC là tia phân giác của A M O ^
Tương tự OD là tia phân giác của B O M ^ suy ra OC ⊥ OD <=> C O D ^
b, Do ∆AOM cân tại O nên OE là đường phân giác đồng thời là đường cao
=> O E M ^ = 90 0 chứng minh tương tự O F M ^ = 90 0
Vậy MEOF là hình chữ nhật
c, Gọi I là trung điểm CD thì I là tâm đường tròn đường kính CD và IO=IC=ID. Có ABDC là hình thang vuông tại A và B nên IO//AC//BD và IO vuông góc với AB. Do đó AB là tiếp tuyến của đường tròn đường kính CD.