Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ABOC có
H là trung điểm của OA
H là trung điểm của BC
Do đó: ABOC là hình bình hành
mà OA=OB
nên ABOC là hình thoi

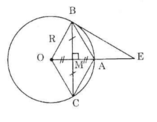
a) Bán kính OA vuông góc với BC nên MB = MC.
Lại có MO = MA (gt).
Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường.
Lại có: OA ⊥ BC nên OBAC là hình thoi.
b) Ta có: OA = OB (bán kính)
OB = BA (tính chất hình thoi).
Nên OA = OB = BA => ΔAOB đều = > ∠ A O B = 60 °
Trong tam giác OBE vuông tại B ta có:
B E = O B . t g ∠ A O B = O B . t g 60 ° = R . √ 3

a: Xét (O) có
BM,BN là các tiếp tuyến
nen BM=BN và BO là phân giác của góc MBN
=>OB là đường trung trực của MN
Xét ΔOMB vuông tại M có sin OBM=OM/OB=1/2
nên góc OBM=30 độ
=>góc MBN=60 độ
b: Xét ΔOMA có OM=OA và góc MOA=60 độ
nên ΔOMA đều
=>OM=OA=AM
Xét ΔONA có ON=OA và góc AON=60 độ
nên ΔONA đều
=>ON=OA=AM
=>OM=AM=ON=AN
=>AMON là hình thoi
c: \(OH=\dfrac{OM^2}{OB}=\dfrac{R^2}{2R}=\dfrac{R}{2}\)