Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

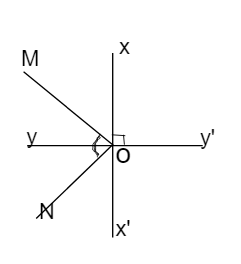
Vì xx' ⊥ yy' tại O (gt)
⇒ ∠x'Oy = 900 (định nghĩa 2 đường thẳng vuông góc)
Ta có: ∠xOy + ∠x'Oy = 1800 (2 góc kề bù)
Thay số: ∠xOy + 900 = 1800
∠xOy = 1800 - 900
∠xOy = 900
Mà OM là tia phân giác của ∠xOy
ON là tia phân giác của ∠yOx'
⇒ ∠mOy = 450
∠yOn = 450
Ta có: ∠mOy + ∠yOn = ∠mOn (2 góc kề nhau)
Thay số: 45+45 = ∠mOn
900 = ∠mOn
∠mOn = 900
Vậy ∠mOn = 900

Ta có: 2 tia xx' và yy' cắt nhau tại O
\(\Rightarrow\widehat{xOy}\) và \(\widehat{yOx'}\) là 2 góc kề bù
\(\Rightarrow\widehat{xOy}+\widehat{yOx'}=180^0\)
Mà \(2\widehat{xOy}=3\widehat{yOx'}\Rightarrow\widehat{yOx'}=\dfrac{2}{3}\widehat{xOy}\)
\(\Rightarrow\widehat{xOy}+\dfrac{2}{3}\widehat{xOy}=180^0\)
\(\Rightarrow\dfrac{5}{3}\widehat{xOy}=180^0\)
\(\Rightarrow\widehat{xOy}=108^0\)
cho hai đường thẳng xx' và yy' cắt nhau tại O. biết x'Oy+xOy'=120o. Tính các góc xOy;yOx';x'Oy';y'Ox


a) ta có O1+O2=180=> O2=180-O1=180-36=144
TA CÓ : O1=O3 =36 ( đối đỉnh )
O2=O4 =144 ( đối đỉnh)
b) ta có góc tOt'= góc tOx+O4+góc y'Ot'= \(\frac{36}{2}\)+144+ \(\frac{36}{2}\)=180
=> Ot và Ot' nằm trên cùng đường thẳng
mặt khác Ot và Ot' cùng chung gốc O
=> Ot và Ot' là 2 tia đối
Hình tự vẽ nha
\(\widehat{xOy}+\widehat{x'Oy}=180^0\left(kề.bù\right)\\ \Rightarrow\widehat{x'Oy}=180^0-70^0=110^0\)
Mà Ot là phân giác \(\widehat{x'Oy}\) nên \(\widehat{x'Ot}=\widehat{yOt}=\dfrac{1}{2}\widehat{x'Oy}=\dfrac{1}{2}\cdot110^0=55^0\)
\(\Rightarrow\widehat{xOt}=\widehat{xOy}+\widehat{yOt}=55^0+70^0=125^0\)