Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(\widehat{EDF}=\widehat{ECF}\) (chắn hai cung bằng nhau AI và BI của đường tròn (O))
\(\Rightarrow\) Tứ giác CDEF nội tiếp
\(\Rightarrow\widehat{DEF}+\widehat{DCF}=180^0\)
Mà \(\widehat{DCF}+\widehat{DAB}=180^0\) (tứ giác ABCD nội tiếp)
\(\Rightarrow\widehat{DEF}=\widehat{DAB}\)
\(\Rightarrow EF||AB\) (hai góc đồng vị bằng nhau)

Ta có \(\widehat{MSE}\) = ![]() (1)
(1)
( vì \(\widehat{MSE}\) là góc có đỉnh S ở trong đường tròn (O))
\(\widehat{CME}\) = ![]() =
= ![]() (2)
(2)
(\(\widehat{CME}\) là góc tạo bởi tiếp tuyến và dây cung).
Theo giả thiết ![]() =
= ![]() (3)
(3)
Từ (1), (2), (3) ta có: \(\widehat{MSE}\)= \(\widehat{CME}\)từ đó \(\Delta\)ESM là tam giác cân và ES = EM

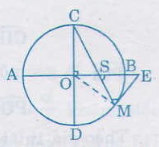
Ta có =
![]() (1)
(1)
( vì là góc có đỉnh S ở trong đường tròn (O))
=
![]() =
= ![]() (2)
(2)
( là góc tạo bởi tiếp tuyến và dây cung).
Theo giả thiết ![]() =
= ![]() (3)
(3)
Từ (1), (2), (3) ta có: =
từ đó ∆ESM là tam giác cân và ES = EM

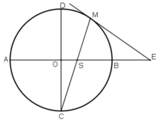
+ M S E ^ là góc có đỉnh S ở trong đường tròn (O)
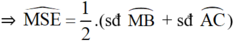
+ E S M ^ là góc tạo bởi tiếp tuyến ME và đây MC
⇒ E M S ^ = 1 2 . s đ M C ⏜ = 1 2 . s đ M B ⏜ + s đ B C ⏜
