Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án: C
Chu kỳ dòng điện T = 2π/ω = 0,02s
Thời gian t =965s = 48250T
Xét trong chu kỳ đầu tiên khi t=0 thì i = π.cos(-π/2) = 0, sau đó i tăng rồi giảm về 0 lúc t = T/2 =0,01s. Sau đó dòng điện đổi chiều chuyển động.
Vậy điện lượng qua bình theo một chiều trong 1 chu kỳ là 
Vậy điện lượng qua bình theo một chiều trong thời gian 16 phút 5 giây là:
Sử sụng hệ thức: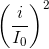 
+
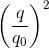= 1
Thay số và giải hệ phương trình trìm I0 và q0
Tần số góc: ω =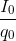 
= 50 (rad/s)
Chú ý trong mạch dao động \(i_1\perp u_1;i_2\perp u_2\)
Mặt khác ta có độ lệch pha giữa hai \(i_1;i_2\):\(t_2-t_1=\frac{\pi}{2}\sqrt{LC}=\frac{T}{4}\Rightarrow\Delta\varphi=\frac{T}{4}.\frac{2\pi}{T}=\frac{\pi}{2}\)
=> \(i_1\perp i_2\)
i i u u 1 1 2 2
Nhìn vào đường tròn ta thấy \(i_1\perp i_2,u_1\perp u_2\); \(i_1\) ngược pha \(u_2\) và ngược lại.
\(\frac{i_1^2}{I^2_0}+\frac{u^2_1}{U_0^2}=1;\frac{i_1^2}{I^2_0}+\frac{i^2_2}{I_0^2}=1;\frac{i_1^2}{I^2_0}+\frac{u^2_2}{U_0^2}=1;\frac{i_2^2}{I^2_0}+\frac{u^2_1}{U_0^2}=1;\)
\(U_0=\frac{I_0}{\omega}\Rightarrow I_0=\omega\sqrt{U_0}=\frac{1}{\sqrt{LC}}\sqrt{U_0}\)
Dựa vào các phương trình trên ta thấy chỉ có đáp án D là sai.
Cường độ dòng điện tức thời qua tụ: \(i=\frac{\Delta q}{\Delta t}=C\frac{\Delta u}{\Delta t}\)
Do 2 tụ mắc song song nên điện áp tức thời 2 đầu mỗi tụ như nhau. Do vậy \(\frac{i_1}{i_2}=\frac{C_1}{C_2}=\frac{1}{2}\Rightarrow i_2=2i_1=2.0,04=0,08A\).
Cường độ dòng điện qua cuộn cảm là: i=i1+i2=0,04+0,08=0,12A
Do năng lượng của tụ: \(W_đ=\frac{1}{2}C.u^2\), nên năng lượng điện tỉ lệ với điện dung C.
Do đó, năng lượng của tụ C1 là: 13,5.10-6 / 2 = 6,75.10-6 (J)
Năng lượng điện của mạch: W = 13,5.10−6+6,75.10-6 =20,25.10-6
Năng lượng điện từ của mạch: \(W=W_đ+W_t=W_{tmax}\Rightarrow 20,25.10^{-6}+\frac{1}{2}.5.10^{-3}.(0,12)^2=\frac{1}{2}.5.10^{-3}.I_0^2\)
=>\(I_0=0,15A\)
Đáp án D
Hướng dẫn:
\(U_{AB}=U_C=2\) (1)
\(U_{BC}^2=U_r^2+U_L^2=3\) (2)
\(U_{AC}^2=U_r^2+(U_L-U_C)^2=1\) (3)
Giải hệ 3 pt trên sẽ tìm đc \(U_r\) và \(U_L\)
Chia cho \(I\) sẽ tìm được \(r\) và \(Z_L\)
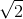
Đáp án: C
Chu kỳ dòng điện T = 2π/ω = 0,02s
Thời gian t =965s = 48250T
Xét trong chu kỳ đầu tiên khi t=0 thì i = π.cos(-π/2) = 0, sau đó i tăng rồi giảm về 0 lúc t = T/2 =0,01s. Sau đó dòng điện đổi chiều chuyển động.
Vậy điện lượng qua bình theo một chiều trong 1 chu kỳ là q = 2 ∫ 0 T / 4 i d t
Vậy điện lượng qua bình theo một chiều trong thời gian 16 phút 5 giây là:
q = 48250 . 2 ∫ 0 T / 4 i d t q = 48250 . 2 ∫ 0 0 . 005 πcos 100 πt - π 2 d t = - 965 C
(lấy độ lớn)