Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Gọi giao của CO với BD là M
Xét ΔOAC vuông tại A và ΔOBM vuông tại B có
OA=OB
góc AOC=góc BOM
=>ΔOAC=ΔOBM
=>OC=OM
Xét ΔDCM có
DO vừa là đường cao, vừa là trung tuyến
nên ΔDCM cân tại D
=>góc DCM=góc DMC=góc ACM
=>CM là phân giác của góc ACD
2: Kẻ OK vuông góc với CD
Xét ΔCAO vuông tại A và ΔCKO vuông tại K có
CO chung
góc ACO=góc KCO
=>ΔCAO=ΔCKO
=>OA=OK=R
=>CD là tiêp tuyến của (O)
3: Kẻ N là trung điểm của CD
Xét hình thang ABDC co
O,N lần lượt là trung điểm của AB,CD
nên ON là đường trung bình
=>ON//AC//BD
=>ON vuông góc với AB
=>AB tiếp xúc với (N)

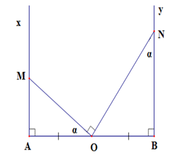
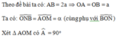
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
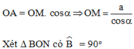
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
![]()
Vậy diện tích tam giác MON là:
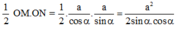
Đáp án cần chọn là: A
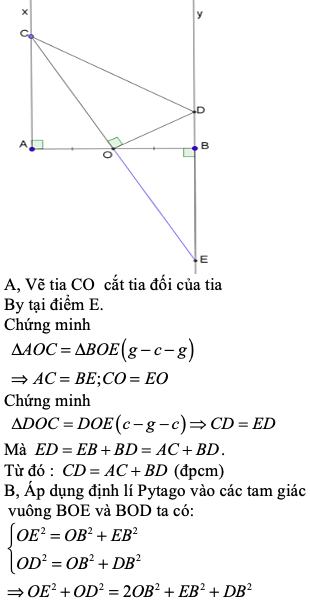
A B x y t z O C D M E F
Ta có
\(\dfrac{OA}{OB}=\dfrac{MC}{MD}=1\) => AC//OM//BD (Talet đảo)
=> ABDC là hình thang
Ta có OA=OB; MC=MD => OM là đường trung bình của hình thang ABDC
\(\Rightarrow OM=\dfrac{AC+BD}{2}\Rightarrow2.OM=AC+BD\)