Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\Delta ABM\)và \(\Delta ECM\)có: BM = MC (M là trung điểm của BC)
\(\widehat{AMB}=\widehat{CME}\)(đối đỉnh)
AM = ME (gt)
=> \(\Delta ABM\)= \(\Delta ECM\)(c. g. c)
b) Ta có \(\Delta ABM\)= \(\Delta ECM\)(cm câu a)
=> AB = EC (hai cạnh tương ứng) (đpcm)
c/ Dựng MI ́ là tia đối của MI
Ta có: \(\Delta AMB=\Delta ECM\)câu a
\(\Rightarrow\widehat{BAM}=\widehat{MEC}\)góc t.ứng
Trong tam giác AMI có: \(\widehat{IAM}+\widehat{AMI}+\widehat{MIA}=180^0\)
Trong tam giác EMI có: \(\widehat{ÍEM}+\widehat{AMÍ}+\widehat{MÍA}=180^0\)
Mà góc IAM = góc I ́EM cmt, Góc AMI = góc AMI ́đối đỉnh. nên góc MIA = góc MI ́A
hay \(\widehat{MIA}=\widehat{MÍA}=90^0\)
Vậy \(MÍ\)vuông góc vs EC hay MI vuông góc vs EC
P/s: chắc đúng

a) Ta có MN vuông góc với AB ( do MN là đường trung trực của đoạn thẳng AB theo giả thuyết nên suy ra)
và đường thẳng m cũng vuông góc với đoạn thẳng AB ( theo giả thiết)
nên từ đó ta suy ra MN//m (đpcm)
b) Từ MN//m ta suy ra MIC=ICB (hai góc so le trong)
mà ICB= 60 độ => MIC=60 độ
c) Ta có HIB= HIN+NIB
Mặt khác HIN=MIC=60 độ ( so le trong)
và NIB=90 độ (gt)
suy ra HIB= 60+90=150 độ
d) Vì theo giả thiết ta có đường thẳng a đi qua C và song song với MN và điểm C lại nằm trên cùng một đường thẳng m với điểm B mà đường thẳng m lại song song với đường thẳng MN nên suy ra đường thẳng a trùng với đường thẳng m và đi qua B

Cậu tự vẽ hình nhé (theo tớ) !! Cho CD là trung trực của AB, O là giao điểm, kẻ 1 điểm M bất kì. Nối A với M, B với M
Bài làm
Xét tam giác AOM và BOM
Có AO = OB (GT)
Góc O1 = O2 ( CD là trung trực của AB)
OM cạnh chung
=> Tam giác AOM = BOM (c.g.c)
=> MA = MB ( 2 cạnh tương ứng )
>> Nhớ cho mik nhé ! ❤

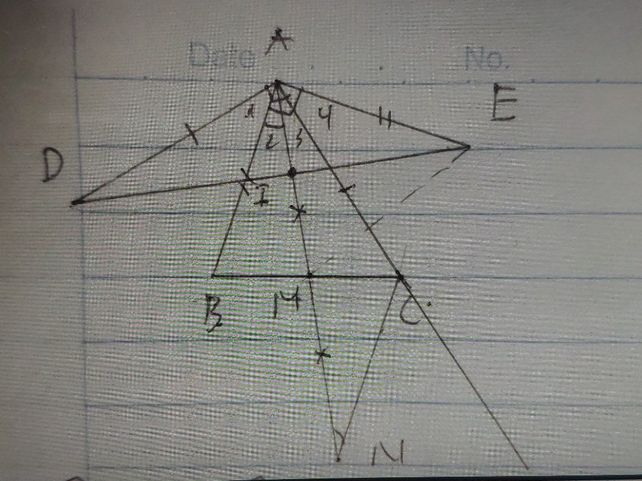
a, Ta có:
góc DAB = góc EAC( Vì cùng phụ góc BAC)
AD= AC
AB=AE
Nên tam giác ABD = tam giác AEC
Vây BD = CEb,
Ta có: ACNB là hình bình hành nên góc ACN + góc BAC = 180độ (1)
Mặt khác ta có : 2( góc DAB +góc BAC) = 2. 90 độ = 180độ
Nên góc DAB + góc EAC + góc BAC + góc BAC = 180 độ
Suy ra DAE + BAC = 180 độ (2)
Từ (1) và (2) ta đc góc DAE = góc ACN
Mà AD = AC; AB= CN nên tam giác ADE = Tam giác cân
c, Ta có: góc NAC = góc ADE ( cmt )
Mà góc NAC + góc DAM = 90 độ nên ADE + góc DAM = 90 độ
Vậy DIA = 90 độ
Áp dụng pytago ta có:\(\frac{AD^2+IE^2}{DI^2+AE^2}=\frac{\left(AD^2+DI^2\right)+\left(AE^2-AI^2\right)}{DI^2+AE^2}=1\)

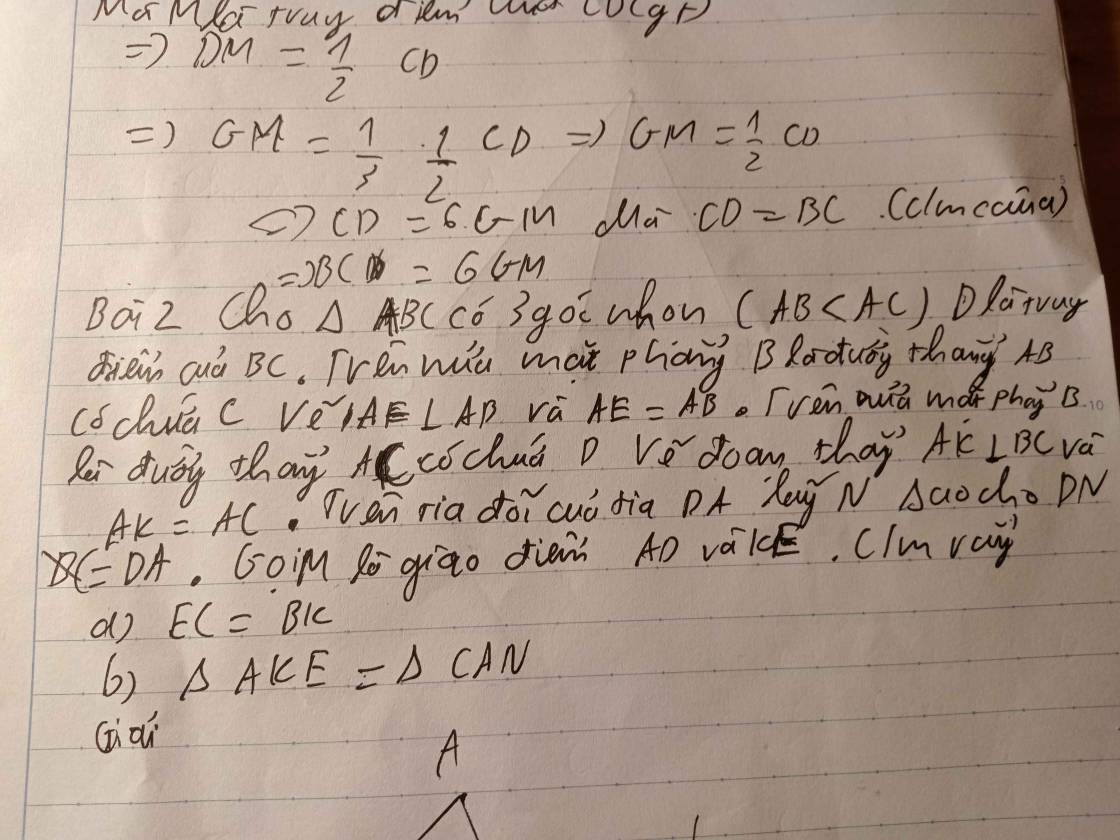
Xét ΔMIA và ΔMIB có
MI chung
IA=IB
MA=MB
Do đó: ΔMIA=ΔMIB
=>\(\widehat{MIA}=\widehat{MIB}\)
mà \(\widehat{MIA}+\widehat{MIB}=180^0\)(hai góc kề bù)
nên \(\widehat{MIA}=\widehat{MIB}=\dfrac{180^0}{2}=90^0\)
=>MI\(\perp\)AB
Ta có:
Góc AIM + BIM = 180 độ(2 góc kề bù)
AIm + BIM = 180
AIm = 180 : 2
AIM = 90
vậy IM vuông góc vs AB