Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
b/ ta có: Góc DAE = 360 - (90 . 2) - góc A = 180 - 110 = 70 độ
từ tam giác ABM = tam giác KCM => AB = CK
Xét tam giác CAK & tam giác AED có:
KCA = DAE (bằng 70 độ)
AD = CK (bằng AB)
AC = AE (gt)
=> tam giác CAK = tam giác AED (cgc)
b, vì tam giác ABM=tam giác KCM(câu a) =>AB=CK(2 cạnh tương ứng)
mà AB=AD(gt) =>KC=AD
Có DAE+DAB+EAC+BAC=3600=>DAE=3600-(DAB+EAC+BAC)
mả DAB=900(AD vuông góc vs AB-GT)
EAC=900(AE vuông góc vs AC-GT)
BAC=1100 (GT)
=>DAE=3600-(900+900+1100)=700
Có DAE=700(CMT)
ACK=700(câu a)
=>DAE=ACK(=700)
Xét tam giác CAK & tam giác AED có:
CK=AD(cmt)
CA=AE(gt)
DAE=ACK(cmt)
=>tam giác CAK=tam giác AED(c.g.c)
phần c mik k bit lm giúp nhé
Có: ∠DAE + ∠DAB + ∠BAC + ∠CAE = 360o
Mà ∠DAB = ∠CAE = 90o; ∠BAC = 110o
⇒ ∠DAE = 70o
⇒ ∠DAE = ∠ACK
+) Xét ΔCAK và ΔAED có:
AC = AE (gt)
∠ACK = ∠DAE (chứng minh trên)
CK = AD (cùng = AB)
⇒ ΔCAK = ΔAED (c.g.c)
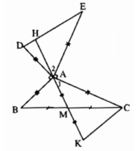
a) Xet tam giac ABM va tam giac CMK ta co:
AM=MK(gt)
BM=MC(M la trung diem BC)
goc AMB=goc KMC ( 2 goc doi dinh)
--> tam giac ABM= tam giac CMK (c-g-c)--> goc BAM = goc MKC hay goc BAM= goc AKC
ta co : goc AKC+goc ACK+goc KAC=180 ( tong 3 goc trong tam giac AKC)
ma goc AKC= goc BAM (cmt)
mem goc BAM+goc KAC+goc ACK=180
--> goc BAC+ goc ACK=180
---> 110+ goc ACK=180
---> goc ACK=180-110=70
b)ta co : goc BAC+goc BAD+ goc DAE+goc CAE=360
----> 110+90+ goc DAE+90=360
---> goc DAE=360-110-90-90=70
-ta co : AB=DA ( gt)
AB=CK ( tam giac ABM= tam giac MKC)
--> DA=CK
xet tam giac CAK va tam giacAED ta co"
CK=DA (cmt) , AC=AE (gt), goc ACK= goc DAE (=70)
--> tam giac CAK= tam giac AED ( c=g=c)
c) Keo dai KA cat DE tai H
ta co : goc HAE + goc EAC+goc CAK=180
ma goc AEH= goc CAK ( tam giac ADE= tam giac CAK)
nen goc HAE+goc AEH=180- goc EAC=180-90=90
ta co : goc HAE+goc AEH + goc AHE =180 ( tong 3 goc trong tam giac AHE)
--> 90+ goc AHE =180
--> goc AHE =180-90=90
--> AH vuong goc DE hay MA vuong goc DE
a) \(\Delta\)ABM = \(\Delta\)KCM (c.g.c) => ^ABM = ^KCM (2 góc tương ứng) => AB // CK (2 góc so le trong bằng nhau)
=> ^BAC + ^ACK = 1800 (2 góc trong cùng phía) => ^ACK = 1800 - 1100 = 700
b) \(\Delta\)ABM = \(\Delta\)KCM (cmt) => AB = KC (2 cạnh tương ứng). Mà AB = AD => CK = AD
Ta có: ^BAC + ^BAD + ^CAE + ^DAE = 3600 => ^BAC + ^DAE = 1800
Mà ^BAC + ^ACK = 1800 => ^DAE = ^ACK hay ^DAE = ^KCA
Xét \(\Delta\)CAK và \(\Delta\)AED có: CK=AD; CA=AE; ^KCA = ^DAE => \(\Delta\)CAK = \(\Delta\)AED (đpcm).
c) Tia MA giao DE tại điểm H.
\(\Delta\)CAK = \(\Delta\)AED (cmt) => ^CAK = ^AED (2 góc tương ứng) hay ^CAK = ^AEH
Mà ^CAK + ^HAE = 1800 - ^CAE = 900 => ^AEH + ^HAE = 900 => \(\Delta\)AHE vuông tại H
=> AH vuông góc với DE hay MA vuông góc DE (đpcm).
