Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Hình vẽ:
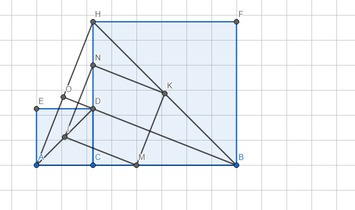
a) -Xét △ACH và △DCB có:
\(AC=DC\) (ACDE là hình vuông).
\(HC=CB\) (BCHF là hình vuông).
\(\widehat{ACH}=\widehat{DCB}=90^0\).
=>△ACH=△DCB (c-g-c).
=>\(AH=BD\) (2 cạnh tương ứng).
*BD cắt AH tại O.
- Ta có: \(\widehat{AHC}=\widehat{DBC}\) (△ACH=△DCB).
Mà \(\widehat{DBC}+\widehat{BDC}=90^0\) (△DCB vuông tại C).
=>\(\widehat{AHC}+\widehat{BDC}=90^0\).
Mà \(\widehat{BDC}=\widehat{ODH}\) (đối đỉnh).
=>\(\widehat{AHC}+\widehat{ODH}=90^0\).
Mà \(\widehat{AHC}+\widehat{ODH}+\widehat{HOD}=180^0\) (tổng 3 góc trong △HOD).
=>\(90^0+\widehat{HOD}=180^0\).
=>\(\widehat{HOD}=90^0\) nên \(AH\perp BD\) tại O.
b) - Xét △ADH có:
I là trung điểm AD (I là tâm đối xứng của hình vuông ACDE).
N là trung điểm DH (gt).
=>IN là đường trung bình của △ADH.
=>IN=\(\dfrac{1}{2}AH\) (1) ; IN//AH
- Xét △ADB có:
I là trung điểm AD (I là tâm đối xứng của hình vuông ACDE).
M là trung điểm AB (gt).
=>IM là đường trung bình của △ADB.
=>IM=\(\dfrac{1}{2}BD\)=\(\dfrac{1}{2}AH\). (2); IM//BD.
- Từ (1) và (2) suy ra: \(IM=IN\)
- Ta có: \(AH\perp BD\) (cmt) ; IN//AH (cmt) ; IM//BD(cmt).
=>\(IN\perp IN\) tại I.
- Xét △DHB có:
K là trung điểm BH (K là tâm đối xứng của hình vuông BCHF).
N là trung điểm DH (gt).
=>KN là đường trung bình của △DHB.
=>KN=\(\dfrac{1}{2}BD\) (3) ; NK//BD.
- Từ (3) và (4) suy ra: KN=IM mà KN//IM//BD.
=>NKMI là hình bình hành mà IM=IN (cmt)
=>NKMI là hình thoi mà \(\widehat{NIM}=90^0\) (\(IM\perp IN\) tại I).
=>NKMI là hình vuông.

Bài 12:
:v Mình sửa P là trung điểm của EG
A B C D E O Q N F G M I 1 2 P
a) Ta có: \(\widehat{EAC}=\widehat{EAB}+\widehat{BAC}=90^0+\widehat{BAC}\)
\(\widehat{GAB}=\widehat{GAC}+\widehat{BAC}=90^0+\widehat{BAC}\)
\(\Rightarrow\widehat{EAC}=\widehat{GAB}\)
Xét tam giác EAC và tam giác BAG có:
\(\hept{\begin{cases}EA=AB\\\widehat{EAC}=\widehat{GAB}\left(cmt\right)\\AG=AC\end{cases}}\Rightarrow\Delta EAC=\Delta BAG\left(c-g-c\right)\)
\(\Rightarrow CE=BG\)( 2 cạnh t. ứng )
+) Gọi O là giao điểm của EC và BG, Gọi I là giao điểm của AC và BG
Vì \(\Delta EAC=\Delta BAG\left(cmt\right)\)
\(\Rightarrow\widehat{ACE}=\widehat{AGB}\)
Vì tam giác AIG vuông tại A nên \(\widehat{I1}+\widehat{AGB}=90^0\)(2 góc phụ nhau )
Mà \(\widehat{ACE}=\widehat{AGB}\left(cmt\right),\widehat{I1}=\widehat{I2}\)( 2 góc đối đỉnh )
\(\Rightarrow\widehat{I2}+\widehat{ACE}=90^0\)
Xét tam giác OIC có \(\widehat{I2}+\widehat{ACE}+\widehat{IOC}=180^0\left(dl\right)\)
\(\Rightarrow\widehat{IOC}=90^0\)
\(\Rightarrow BG\perp EC\)
b) Vì ABDE là hình vuông (gt)
\(\Rightarrow EB\)cắt AD tại Q là trung điểm của mỗi đường (tc)
Xét tam giác EBC có Q là trung điểm của EB (cmt) , M là trung điểm của BC (gt)
\(\Rightarrow QM\)là đường trung bình của tam giác EBC
\(\Rightarrow QM=\frac{1}{2}EC\left(tc\right)\)
CMTT: \(PN=\frac{1}{2}EC;QP=\frac{1}{2}BG,MN=\frac{1}{2}BG\)
Mà EC=BG (cm câu a )
\(\Rightarrow QM=MN=NP=PQ\)
Xét tứ giác MNPQ có \(QM=MN=NP=PQ\left(cmt\right)\)
\(\Rightarrow MNPQ\)là hình thoi ( dhnb ) (1)
CM: MN//BG , QM//EC ( dựa vào đường trung bình tam giác )
Mà \(BG\perp EC\left(cmt\right)\)
\(\Rightarrow MN\perp MQ\)
\(\Rightarrow\widehat{QMN}=90^0\)(2)
Từ (1) và (2) \(\Rightarrow MNPQ\) là hình vuông ( dhnb )
\(\)
Bài 11:
A B C H D P E Q
a) Ta có: \(\widehat{HAD}+\widehat{HAE}=90^0+90^0=180^0\)
\(\Rightarrow\widehat{DAE}=180^0\)
\(\Rightarrow D,A,E\)thẳng hàng
b) Vì AHBD là hình chữ nhật (gt)
\(\Rightarrow AB\)cắt DH tại trung điểm mỗi đường (tc) và AB=DH(tc)
Mà P là trung điểm của AB (gt)
\(\Rightarrow P\)là trung điểm của DH (1)
\(\Rightarrow PH=\frac{1}{2}DH,PA=\frac{1}{2}AB\)kết hợp với AB=DH (cmt)
\(\Rightarrow PH=PA\)
\(\Rightarrow P\in\)đường trung trục của AH
CMTT Q thuộc đường trung trực của AH
\(\Rightarrow PQ\)là đường trung trực của AH
c) Từ (1) => P thuộc DH
=> D,P,H thẳng hàng
d) Vì ABCD là hình chữ nhật (gt)
=> DH là đường phân giác của góc BHA (tc) mà góc BHA= 90 độ
=> góc DHA= 45 độ
CMTT AHE =45 độ
=> góc DHA+ góc AHE=90 độ
Hay góc DHE=90 độ
=> DH vuông góc với HE

https://lazi.vn/edu/exercise/cho-tam-giac-abc-goi-d-e-f-theo-thu-tu-la-trung-diem-cua-ab-bc-ca-goi-m-n-p-q-theo-thu-tu-la-trung-diem
Bạn xem tại link này nhé
Học tốt!!!!!!

A B C H D E M N I
a) Tứ giác AEHD có 3 góc vuông nên góc còn lại cũng vuông \(\Rightarrow\) tứ giác AEHD là hình chữ nhật.
b)Ta cần chứng minh NA = AM và A, M, N thẳng hàng
Do tứ giác AEHD là hình chữ nhật nên AD // EH \(\Rightarrow\)AD//NE (1)
Mặt khác DE là đường trung bình nên DE // NM \(\Rightarrow\)DE //NA(2)
Từ (1) và (2) suy ra tứ giác EDAN là hình bình hành \(\Rightarrow\) ED = AN (*)
Tương tự ED = AM (**) .Từ (*) và (**) suy ra AM = AN (***)
Dễ chứng minh \(\Delta\)MAD = \(\Delta\)HAD \(\Rightarrow\)^MAD = ^HAD (4)
Tương tự: ^NAE = ^HAE (5) . Cộng theo vế (4) và (5) suy ra ^MAD + ^NAE = 90o (6)
Từ (6) suy ra ^MAD + ^NAE + ^EAD = 90o + ^EAD = 180o \(\Rightarrow\)N, A, E thẳng hàng (****)
Từ (***) và (****) suy ra đpcm.
c)\(\Delta\)ABC vuông tại A có AI là trung tuyến nên \(AI=\frac{1}{2}BC=CI\)\(\Rightarrow\)\(\Delta\)ACI cân tại I
\(\Rightarrow\)^IAC = ^ICA (7)
Mặt khác ta dễ dàng chứng minh \(\Delta\)CNA = \(\Delta\)CHA (tự chứng minh đi nhé!)
Suy ra ^NCA = ^HCA \(\Rightarrow\)^NCA = ^ICA (8) (vì H, I cùng thuộc B nên ta có H, I, C thẳng hàng do đó ^HCA = ^ICA)
Từ (7) và (8) ta có ^IAC = ^NCA. Mà hai góc này ở vị trí so le trong nên ta có đpcm.
P/s: Không chắc nha!

Bài 1:
A B C D M N P Q E F
a) Xét tam giác ABC có M là trung điểm của AB (gt) ,E là trung điểm của AC (gt)
\(\Rightarrow ME\)là đường trung bình tam giác ABC
\(\Rightarrow ME=\frac{1}{2}BC\left(tc\right)\left(1\right)\)
Xét tam giác ADC có E là trung điểm của AC (gt) ,P là trung điểm của DC (gt)
\(\Rightarrow PE\)là đường trung bình của tam giác ADC
\(\Rightarrow PE=\frac{1}{2}AD\left(tc\right)\left(2\right)\)
mà \(AD=BC\left(gt\right)\left(3\right)\)
Từ (1) , (2) và (3) \(\Rightarrow EM=PE\)
CMTT: \(PE=FP,FM=ME\)
\(\Rightarrow ME=EP=PF=FM\)
Xét tứ giác MEPF có:
\(ME=EP=PF=FM\left(cmt\right)\)
\(\Rightarrow MEPF\)là hình thoi ( dhnb)
b) Vì \(MEPF\)là hình thoi (cmt)
\(\Rightarrow FE\)giao với MP tại trung điểm mỗi đường (tc) (4)
Xét tam giác ADB có M là trung điểm của AB(gt) ,Q là trung điểm của AD (gt)
\(\Rightarrow MQ\)là đường trung bình của tam giác ADB
\(\Rightarrow MQ//DB,MQ=\frac{1}{2}DB\left(tc\right)\left(5\right)\)
Xét tam giác BDC có N là trung điểm của BC(gt) , P là trung điểm của DC(gt)
\(\Rightarrow NP\)là đường trung bình của tam giác BDC
\(\Rightarrow NP//DB,NP=\frac{1}{2}DB\left(tc\right)\left(6\right)\)
Từ (5) và (6) \(\Rightarrow MQ//PN,MQ=PN\)
Xét tứ giác MQPN có \(\Rightarrow MQ//PN,MQ=PN\)
\(\Rightarrow MQPN\)là hình bình hành (dhnb)
\(\Rightarrow MP\)giao QN tại trung điểm mỗi đường (tc) (7)
Từ (4) và (7) \(\Rightarrow MP,NQ,EF\)cắt nhau tại một điểm
c) Xét tam giác ABD có Q là trung điểm của AD (gt), F là trung điểm của BD(gt)
\(\Rightarrow QF\)là đường trung bình của tam giác ADB
\(\Rightarrow QF//AB\left(8\right)\)
CMTT: \(FN//CD\)và \(EN//AB\)
Mà Q,F,E,N thẳng hàng
\(\Rightarrow AB//CD\)
Vậy để Q,F,E,N thẳng hàng thì tứ giác ABCD phải thêm điều kiện \(AB//CD\)
a, Ta có tam giác ACH = tam giác DCB (do HC=CB và AC=DC và là 2 tam giác vuông )
---> AH=DB và góc CHA = góc CBD
Mà góc CHA +góc CAH =90 độ
---> góc CBD + góc CAH =90 độ
-----> BD vuông AH
b, Xét tam giác ADB có I là trung điểm của DA,Ml là trung điểm của AB
------> IM là đường tb của tam giác DAB --> IM // DB (1)
Gọi giao của BD và AH là T
Ta lại có Tam giác HTB có N là trung điểm của HT , K là trung điểm của HB
----> N là đường trung bình của tam giác HTB---> NK//TB//TB hay NK//DB (2)
Từ (1),(2)--> NK//IM
---> Tam giác IMKN là hình bình hành
Lại có IM// DB mà DB vuông HA --> IM vuông HA
---> NKMI là hình chữ nhật